Show Intermediate Field: Q[i.rt(6)] Between F & Q

[Firepanda]

How do I go about showing a field is intermediate between two others?

For example I'm trying to do this question:

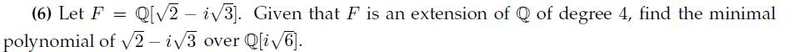
But first of all I'm trying to find the degree of the extension [F:Q[i.rt(6)]]

How can I show that Q[i.rt(6)] is an intermediate field?

 

[Office_Shredder]

It's obviously contains Q because, well it contains Q. It's contained in \mathbb{Q}[\sqrt{2}-i\sqrt{3}] because (\sqrt{2}-i\sqrt{3})^2=2-2i\sqrt{6}-3 (try to work out the details if that doesn't make it obvious).