bckcookie
- 17
- 0
Homework Statement
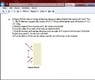
As attached file! Please advise me my solution is right or not! Thanks a lot!
Homework Equations
F=qvB - (1)
R=mv/eB
d/t = v
length of arc = 2pi(R)
sinθ=a/c
The Attempt at a Solution
a) the magnetic force,
F = qvb
=1.6x10^-19 x 10^7 x 0.03N
= 4.8x10^-14N
(does it need to product with sin 45degree?? please advise!)
b) the radius of curvature
R = mv/eB
= (9.11 x 10^-31kg x 10^7) / 1.6x10^-19 x 0.03
=1.90 x 10^-3m
c) The time spend
=The length of arc / v
= 2∏R / v
= 1.194 x 10^-9s
d) the distance of x
= 2Rsin45
= 2.687 x 10^-3 m