hrf2
- 5
- 0
This is a really abstract question, and I'm absolutely clueless on how to approach it.
I know W= F*d, where F=force and d=distance, as well as W= PEa-PEb.
The question reads:
The diagram shows an isolated point charge. Marked are four paths (A, B, C, and D) from a point (P1) to point (P2). The two points, P1 and P2, are equidistant from the charge. Rank the paths by the work required to move a positive charge from P1 to P2 from least to greatest.
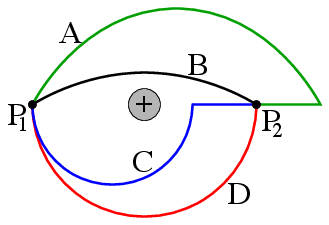
For some reason I feel like B will be the greatest, but I don't really have any basis for that to be honest.
I know W= F*d, where F=force and d=distance, as well as W= PEa-PEb.
The question reads:
The diagram shows an isolated point charge. Marked are four paths (A, B, C, and D) from a point (P1) to point (P2). The two points, P1 and P2, are equidistant from the charge. Rank the paths by the work required to move a positive charge from P1 to P2 from least to greatest.
For some reason I feel like B will be the greatest, but I don't really have any basis for that to be honest.