Messy threads, this one and the -- 98% identical to this one --
other thread which I find a lot more sensible.
The note in post #4 here clarifies a few things -- and messes up others.
- Haru fixed the first 'If P is below' which should have been 'at'.
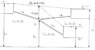
- The term 'elevation of P' confused me no end
I'm not used to working in terms of 'head', only with pressure, but I think 'elevation of P' is the same as ##H_J## and then ##P_D## is understandably the pressure at D .
What P is I find declared nowhere (whatever happened to 'all variables and given/known data' in the template -- my addition: including the dimensions )

?
That would make for ##\ \ H_J = P = Z_D + P_D/(\rho g)\ \ ## (so
not ##\ \ Z_D + P_D/\rho \; g \ \ ##, nitpicking, I know) and now I'm still a bit dazzled but back in the race.
- 'the pipes are sufficiently long that we can neglect minor losses and velocity head' also is cryptic to me. long ? or wide ? The idea is to ignore friction loss (viscosity = 0) ? But why ignore 'velocity head' - when ##V^2/g## is featuring clearly in the other thread ? Or is velocity head something else than this term from the Bernoulli equation ?
@haruspex, could you look at the other thread, see if it is identical and if so, see if the combination makes sense ?
![DSC_0015[1].JPG](/data/attachments/83/83354-1e6d48764f6e4dbee4fb74ed890a5a24.jpg?hash=Hm1Idk9uTb)