Kinematics of Rigid Bodies:Calculating Angular Velocity

AI Thread Summary
The discussion focuses on calculating the angular velocity magnitude of member BC in a rigid body problem. The user initially attempts to use the equation V = ωr but encounters difficulty determining the radius of the disc. It is clarified that the radius at point C is 0.4 m, which can be used with the angular speed to find the velocity at that point. There is also a mention of a slope indicator "4|_ 3," suggesting it relates to the orientation of member BC. The conversation emphasizes the importance of understanding the geometry and relative motion in solving the problem.
pronep
Messages
3
Reaction score
0

Homework Statement



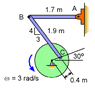
What is the angular velocity magnitude of member BC?

Problem Figure Attached:

Homework Equations


V = w r
Va= Vb + Va/b

The Attempt at a Solution


I thought the problem would be simple as I could use v=w r to calculate the velocity and then use the equation of relative motion to calculate BC...But I am stuck trying to figure out the radius of the disc... Help please..
 

Attachments

  • kinematics.gif
    kinematics.gif
    2.9 KB · Views: 537
Physics news on Phys.org
The full radius of the disk is not necessary. The radius at point C is given as .4 m. That with the angular speed gives the momentary velocity of point C. I'm assuming that the "4|_ 3" thingy is giving the slope of BC at that moment?
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Existential dilemma on angular velocity of a complex rigid body
Replies
25
Views
2K
Solve Angular Velocity & Acceleration - Dimensional Analysis
Replies
3
Views
2K
Angular Momentum- Conserved or not?
Replies
17
Views
357
System of two wheels of different sizes with an axle through their centers
2
Replies
67
Views
4K
The final velocity of a ball rolling while slipping.
Replies
40
Views
4K
What is the final angular velocity of each cylinder
Replies
1
Views
2K
Problem in understanding angular momentum of a rigid body
Replies
10
Views
2K
Brownian Ratchet (exercise framed by Feynman's Lectures, l. 46)
Replies
32
Views
2K
Relating Linear and Angular Kinematics
Replies
3
Views
2K
Kinematics in multiple frames
Replies
10
Views
858

Hot Threads

Recent Insights

Back
Top