You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Kinetics of Masses on an Inclined Plane: Explaining Different Movements
- Thread starter darkmagic
- Start date
-
- Tags
- Kinetics
AI Thread Summary
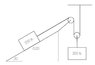
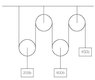
The discussion focuses on understanding the movement of two blocks on an inclined plane connected by a pulley system. It explains that the 300lb block moves only half the distance of the 200lb block due to the mechanics of the pulley, which requires double the string length for the block on the slope to move. Consequently, this halving of distance results in a corresponding halving of both velocity and acceleration. To determine the direction of movement and compute acceleration, participants are advised to analyze the forces acting on each mass using F = ma equations. The conversation emphasizes the importance of understanding the relationship between the pulley movement and the lengths of the strings involved.
Physics news on Phys.org
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
Hi darkmagic! 
velocity = dx/dt and acceleration = d2x/dt2, so if you halve x, you halve velocity and acceleration also.
(and of course x is halved because the pulley moves only half as far as the string)
velocity = dx/dt and acceleration = d2x/dt2, so if you halve x, you halve velocity and acceleration also.
(and of course x is halved because the pulley moves only half as far as the string)
darkmagic
- 164
- 0
how can you know that the pulley moves only half of the string?
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
When the pulley goes down 1 cm, that makes the string above it 1 cm longer on both sides, which requires 2 cm of string, so the block on the slope moves 2cm. 
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
Just ask yourself, does the pulley move? if it does, how many strings are attached? (because each string will have to get longer or shorter by the same distance)
darkmagic
- 164
- 0
yes the blocks will move. my problem is in which direction will they move?
tiny-tim
Science Advisor
Homework Helper
- 25,837
- 258
To find out, write the F = ma equations for each of the three masses.
(and, if the heights of the masses are x y and z, you'll need a linear equation connecting x y and z)
(and, if the heights of the masses are x y and z, you'll need a linear equation connecting x y and z)
Similar threads
- Replies
- 5
- Views
- 3K
- Replies
- 22
- Views
- 4K
- Replies
- 7
- Views
- 1K
Engineering
Control System mass spring damper
- Replies
- 0
- Views
- 1K
- Replies
- 2
- Views
- 3K
- Replies
- 21
- Views
- 4K
- Replies
- 5
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 13
- Views
- 2K
- Replies
- 13
- Views
- 3K
Hot Threads
-
Engineering Why is my output current so low in this Transconductance Amplifier cell?
- Started by arhzz
- Replies: 13
- Engineering and Comp Sci Homework Help
-
LTspice: Implementing a Single Balanced BJT Mixer
- Started by SumDood_
- Replies: 17
- Engineering and Comp Sci Homework Help
-
Max water pressure allowable on solar panels
- Started by ethanesh
- Replies: 16
- Engineering and Comp Sci Homework Help
-
Spiral scissor lift statics
- Started by carlcla
- Replies: 4
- Engineering and Comp Sci Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math