Decimal
- 73
- 7
Homework Statement
[/B]
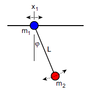
In a homogeneous gravity field with uniform gravitational acceleration g,
a pointmass m1 can slide without friction along a horizontal wire. The mass m1 is the pivot point of a
pendulum formed by a massless bar of constant length L, at the end of which a
second pointmass m2 is attached. m2 can oscillate within the plane. I included a drawing.
Find the equations of motion for this system
Homework Equations
[/B]
Lagrangian
$$ \mathcal{L} = T - V $$
Lagrange equations
$$\frac {d} {dt} (\frac {d\mathcal{L}} {\dot {dq_i}}) - (\frac {d\mathcal{L}} {dq_i}) = 0 $$
Conjugate momenta
$$p_i = (\frac {d\mathcal{L}} {\dot {dq_i}}) $$
$$\dot {p_i} = (\frac {d\mathcal{L}} {dq_i}) $$
The Attempt at a Solution
[/B]
First I computed the kinetic energy and potential energy. $$ T = \frac {1} {2} \dot {x_1}^2*(m_1+m_2) + m \dot {x_1} \dot {\phi} L cos(\phi) + \frac {1} {2} m_2 L^2 \dot {\phi}^2 $$ and $$ V = -m*g*L*cos(\phi) $$ Now I can calculate the Lagrangian: $$ \mathcal{L} = \frac {1} {2} \dot {x_1}^2*(m_1+m_2) + m \dot {x_1} \dot {\phi} L cos(\phi) + \frac {1} {2} m_2 L^2 \dot {\phi}^2 - -m*g*L*cos(\phi) $$ From this I can calculate the conjugate momenta, which then equal: $$ p_{x1} = \dot {x_1} (m1+m2) + m_2 \dot {\phi} L cos(\phi) $$ $$ p_\phi = m_2 L^2 \dot {\phi} + m_2 \dot {x_1} L cos(\phi) $$ Now using the lagrange equations I find the following equations of motion: $$ \ddot {x_1} (m1+m2) + m_2 \ddot {\phi} L cos(\phi) - m_2 \dot {\phi}^2 L sin(\phi) = 0 $$ $$ m_2 L^2 \ddot {\phi} + m_2 \ddot {x_1} L cos(\phi) - m_2 * \dot {x_1} \dot {\phi} L sin(\phi) = -m_2 g L sin(\phi) $$ Now straight up solving these equations for ## \ddot {x_1}## and ##\ddot {\phi}## will take quite a lot of work, so I was wondering whether there is an easier way to get the answer without solving this system directly. I feel like I should to do something with the fact that ## \dot {p_{x1}} = 0 ## so ##p_{x1}## is conserved. I am just not quite sure how I can use this. Help would be greatly appreciated!
Thanks!
Attachments
Last edited: