PaBlo14101066
- 4
- 1
I must find the Lagrangian for an undamped pendulum using the diagram showed below, I've no idea what to do with the second angle φ2 because is measured from the line that joins the two pivot points.
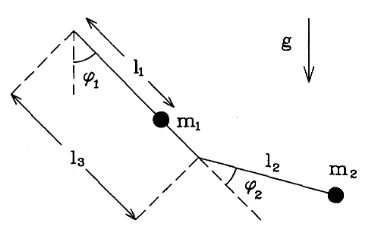
The ecuations I must obtain are as follows
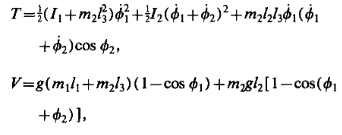
I get so many different things but I can't reach the desired result
The ecuations I must obtain are as follows
I get so many different things but I can't reach the desired result