gpsimms
- 30
- 1
Hi there,
Hopefully this is a very easy question and you all can just confirm this for me.
When calculating heat transfer into a fluid from a heated tube, is it correct to say that the heat transfer coefficient is *not* dependent on the tube diameter?
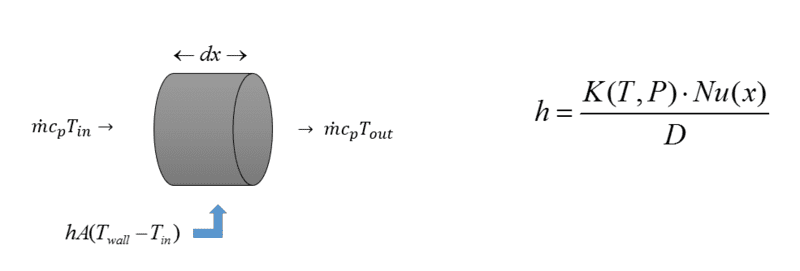
So, if we solve for T_{out}, we get:
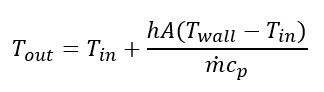
Substituting h for K*N/D, which is fluid thermal conductivity K, Nusselt number (depends on flow conditions and location in flow), and D is diameter, we get:
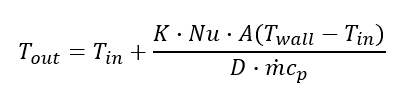
Finally, for our circular duct, A = pi*D*dx, so we get:
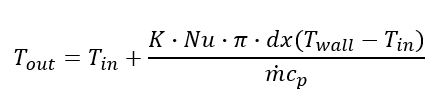
So, is there no dependence on tube diameter? I know that Nusselt number is *weakly* dependent on diameter when the flow is still developing, but that seems like it. In other words, given a large enough furnace, I could put a tube of any size in that furnace, and the flow would heat just as quickly regardless of tube diameter. That feels wrong to me, is there something I am missing?
Thanks!
Hopefully this is a very easy question and you all can just confirm this for me.
When calculating heat transfer into a fluid from a heated tube, is it correct to say that the heat transfer coefficient is *not* dependent on the tube diameter?
So, if we solve for T_{out}, we get:
Substituting h for K*N/D, which is fluid thermal conductivity K, Nusselt number (depends on flow conditions and location in flow), and D is diameter, we get:
Finally, for our circular duct, A = pi*D*dx, so we get:
So, is there no dependence on tube diameter? I know that Nusselt number is *weakly* dependent on diameter when the flow is still developing, but that seems like it. In other words, given a large enough furnace, I could put a tube of any size in that furnace, and the flow would heat just as quickly regardless of tube diameter. That feels wrong to me, is there something I am missing?
Thanks!