Lattice systems and group symmetries

[fyw]

Dear all,

In Marder's Condensed matter physics, it uses matrix operations to explain how to justify two different lattice systems as listed in attachment.

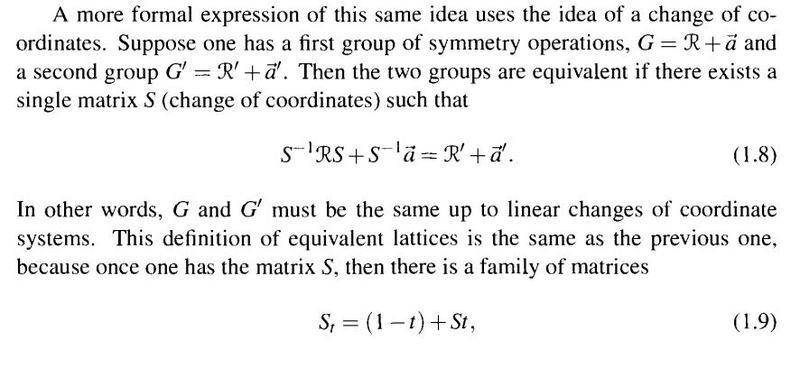
However, I cannot understand why the two groups are equivalent if there exists a single matrix S satisfying S^-1RS^-1+S^-1a=R^'+a^'.

Can someone help me to understand it? Thank you.

 

[Greg Bernhardt]

I'm sorry you are not generating any responses at the moment. Is there any additional information you can share with us? Any new findings?

 

[UltrafastPED]

Marder is saying that if there is a linear map between the two lattice systems, then they are equivalent. The original system is defined by a Rotation (R) and a translation (a).

The matrix S and its inverse are performing a similarity transformation (coordinate system change) on R, and also apply it to the translation.

Marder then notes if there exists one such linear transform, then there exists a family of them.

Personally I found Marder too abstract for my taste, though the group theoretical approach to crystallography is very powerful. But most of the math is not very difficult - it just appears dense because of the writing style.