Law of gravitation and net gravitational force

[jperk980]

[SOLVED] Law of gravitation

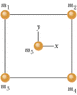
In Figure 13-34, a square of edge length 15.0 cm is formed by four spheres of masses m1 = 5.00 g, m2 = 4.00 g, m3 = 1.50 g, and m4 = 5.00 g. In unit-vector notation, what is the net gravitational force from them on a central sphere with mass m5 = 2.10 g?

I know that since the mass of 1 and 4 are equal they cancel out and i know that the radius is .075*Square root(2). which gives me .106m. I use the equation Gm2m5/r25^2+Gm3m5/r35^2 and i get the answer 6.85e-14 which is not the right answer. I know that the masses are .004, .0015, and .0021 since they are in grams. Can some one help me

 

[Doc Al]

(1) You didn't provide the figure, but I assume that m1 and m4 are at adjacent corners not opposite corners. So they don't cancel out.
(2) The forces are vectors and must be added as such. Direction counts!

 

[jperk980]

sorry Doc Al M1 and M$ are on opposite corners here is the picture given

 

[Doc Al]

OK. Realize that the forces due to m2 and m3 point in opposite directions.

 

[jperk980]

that should mean i should subtract their forces but i tried that and that did not work i got a value of 3.11e-14 which is also incorrect

 

[Doc Al]

I get the same answer. But that's the magnitude of the force. They asked for the force in unit vector notation, which means they want x and y components.

 

[jperk980]

But how would i do that I know how to go from unit vector notation but i do not understand how to do the opposite

 

[Doc Al]

Just find the x and y components of the net force. What direction is that force? What angle does it make with the x-axis?

 

[jperk980]

It is moving towards mass 2 and the angle should be 45

 

[Doc Al]

It is moving towards mass 2 and the angle should be 45

Right. So what are the x and y components of a vector at an angle of 45 degrees to the horizontal?

 

[jperk980]

so i set up the sin 45=o/h and solve so i get hsin 45=0 and i get 2.64e-14 but that is not the correct answer. i do the same thing with cos and get 1.63e-14. where should i go from here

 

[Doc Al]

If a force F makes an angle \theta with the x-axis, its components are:

F_x = F \cos \theta

F_y = F \sin \theta

 

[jperk980]

Isn't that what i did, i just wrote it in different terms

 

[Doc Al]

Isn't that what i did, i just wrote it in different terms

How did you get different answers? (\sin 45 = \cos 45.)

 

[jperk980]

ooo i am in radian mode

 

[jperk980]

Thank you Doc Al for your help