Bublifuk
- 5
- 0
Hello.
I tried to solve this question:
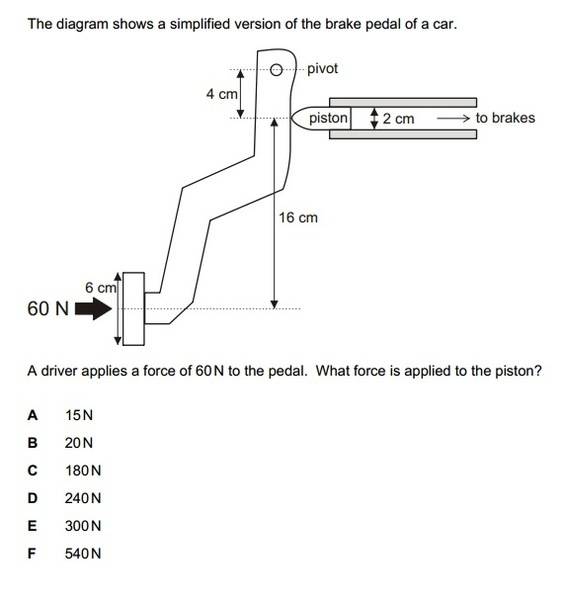
So F1D1=F2D2. Thus:
60N/ 0,06m x 0,2 m= f/0,02m x 0,04m
=100 Newton applied to the piston, but this doesn't fit to the answers offered.
What did I wrong?:(
I tried to solve this question:
So F1D1=F2D2. Thus:
60N/ 0,06m x 0,2 m= f/0,02m x 0,04m
=100 Newton applied to the piston, but this doesn't fit to the answers offered.
What did I wrong?:(