Likelihood, posterior, prior interpretation and credibility/confidence

[fab13]

TL;DR Summary

I am looking for explanations about an article that I have to study. This concerns differents figures that I try to understand and the underlying method that allows to produce these plots.

I try to understand the following article :

testing general relativity from curvature and energy contents at cosmological scale

I don't understand the title of figure 1 :

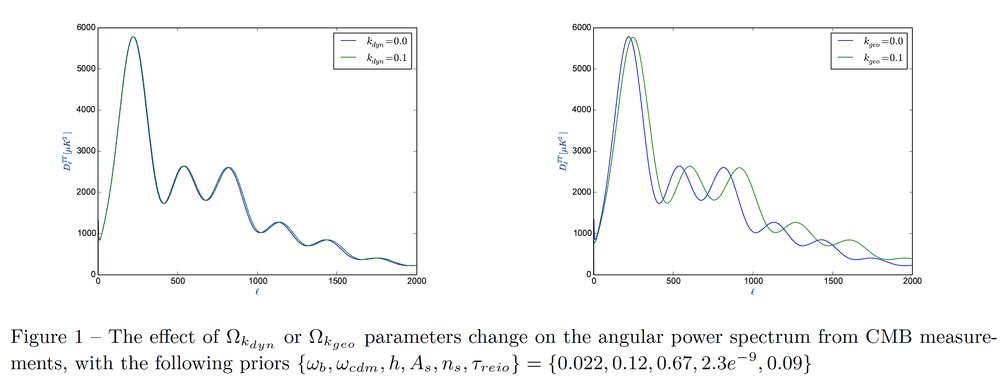
where it is indicated the prior values for $\omega_{b}, \omega_{\text{cdm}}, \text{h}, ...$ : what do authors mean by "prior ?

1) Does this term "prior"refer to the bayesian formula :

\begin{equation}
\text{posterior}= \dfrac{\text{likelihood}\,\times\,\text{prior}}{\text{evidence}}\quad(1)
\end{equation}

which, I think, corresponds to the formula :

\begin{equation}
p(\theta|d)={\dfrac{p(d|\theta)p(\theta )}{p(d)}}\quad(2)
\end{equation}

where $\theta$ is the parameter to estimate and $d$ represent the data

?

So, if this is the case, the prior of parameter $\theta_{i}$ would represent the probability of parameter $p(\theta_{i})$, wouldn't it ?

2.1) On the figure 3 :

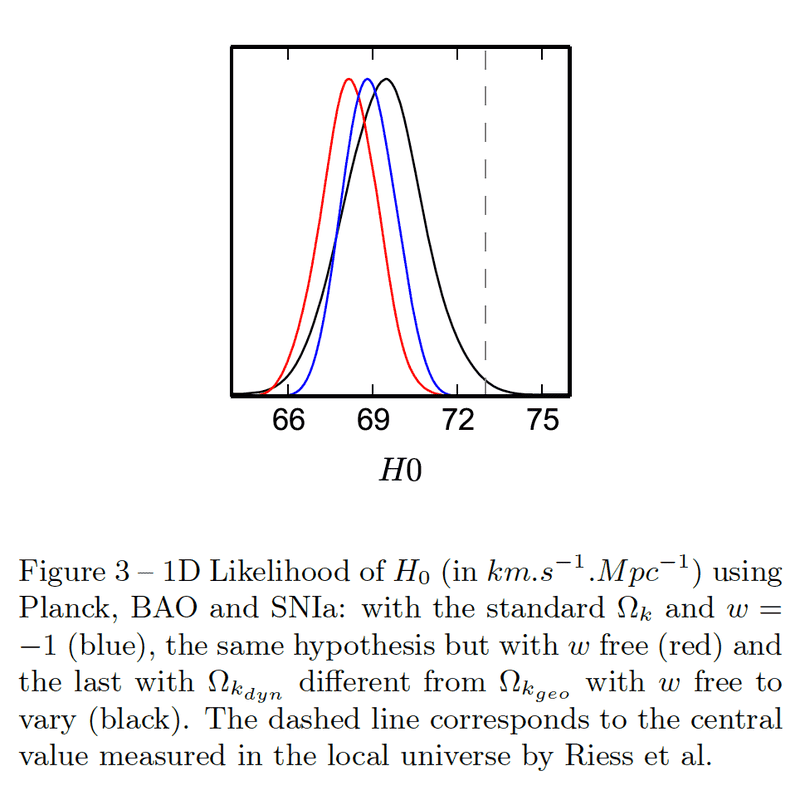
I don't understand how to get this figure :

Given Likelihood is proportional to posterior (is it right from above equation $(1)$ ?), I have to know the theoretical model to compute Likelihood ?

I mean, to get $p(\theta|d)$, I have to generate the probability $p(d|\theta)$ assuming I know the value of $\theta$ parameter, don't I ?

there seems here a paradox : I compute the posterior $p(\theta|d)$ to estimate $\theta$ parameter on one side but I have to know precisely the probability $p(\theta)$


2.2) Moreover, how to compute on this figure the Likelihood of red and black curves which corresponds respectively with parameter $w$ free and $(\Omega_{k},\Omega_{dyn})$ with also free ?

I don't know which theoretical model (I suppose there is a specific PDF (probability function)) to use ? but which one ?

3) Finally, I have a last question about Confidence level (CL with frequentist approach) and Credibility level (Bayesian approach) :

How to make the link between these 2 notions (if this is possible since into a previous post, one told me there is no link except both represent an uncertainty on a variable (either random or parameter)) ?

$\Rightarrow$ the first one is an interval on a random variable and the second one is an interval about the estimation of a parameter, so at first sight, this would't have the same signification.

However, I often see the notion of "Confidence level" for estimation of a parameter (i.e so from a bayesian point of view), like for example the contours on figure 4 of the article cited above, i.e o this figure :

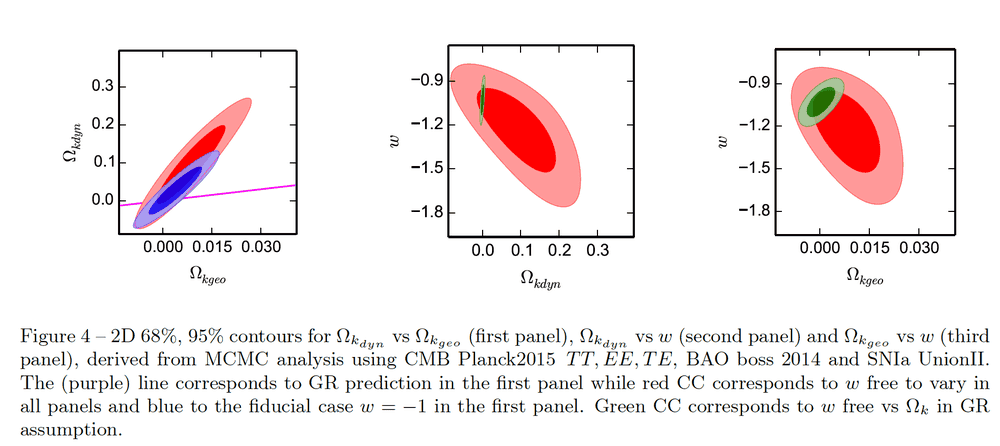
Any help or explanations are welcome, I am very interested in understanding all these concepts of statistics.

Regards

 

[AndyW]

Thank you for your interest in understanding the article on testing general relativity at cosmological scale. I am happy to help clarify the concepts you mentioned.

1) The term "prior" in this context refers to the prior probability distribution of the parameters in the cosmological model being tested. In the context of Bayesian statistics, the prior represents the knowledge or beliefs about the parameters before any data is observed. It is a subjective choice and can be based on previous studies, theoretical expectations, or expert opinions.

2) In figure 3, the likelihood is not directly proportional to the posterior. The likelihood function represents the probability of obtaining the observed data given a specific set of parameters. In order to compute the likelihood, you would need a theoretical model that relates the parameters to the observed data. This can be done using theoretical predictions or simulations. The red and black curves in the figure represent different theoretical models with different sets of parameters. The likelihood of each model is computed by comparing the observed data to the model predictions.

3) Confidence level and credibility level are two different concepts in statistics. Confidence level is a frequentist concept that represents the probability that a confidence interval contains the true value of the parameter. Credibility level is a Bayesian concept that represents the probability that the true value of the parameter falls within a credible interval. Both concepts represent uncertainty in the estimation of a parameter, but they are calculated differently and have different interpretations.

I hope this helps clarify the concepts in the article. If you have any further questions, please don't hesitate to ask. Keep up the curiosity and interest in statistics!