robertjford80
- 388
- 0
line integral -- confusion on squares and square root terms
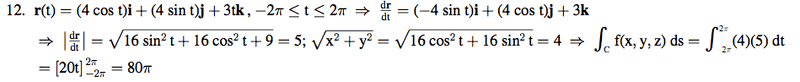
Do you see where they have sqrt(16 sin^2t etc = 5? How do they get that, the answer should be 7, the square root of 16 is 4, sin^2 + cos^2 is 1 and the square root of 9 is 3, 3 + 4 = 7. It's like they're taking the square root of 16 twice.
Homework Statement
Do you see where they have sqrt(16 sin^2t etc = 5? How do they get that, the answer should be 7, the square root of 16 is 4, sin^2 + cos^2 is 1 and the square root of 9 is 3, 3 + 4 = 7. It's like they're taking the square root of 16 twice.