- #1
Saladsamurai
- 3,020
- 7
Line Integrals (yayyy!)
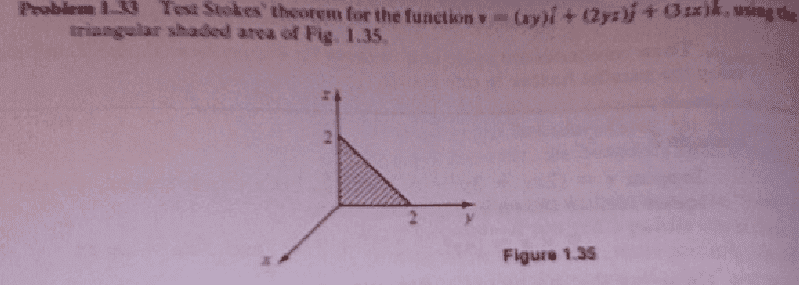
Okay, so I have already done it using the surface integral; now I need to compute the 3 individual line integrals.
By definition, the integral (I will call it I since I am that creative) is given by:
[itex]I=\oint v\cdot\, dl[/itex]
[itex]v=<xy, 2yz, 3xz>[/itex]
[itex]dl=<dx, dy, dz>[/itex]
[itex]\Rightarrow v\dot dl=xydx+2yzdy+3xzdz[/itex]
So the three individual integrals are:
along the base of the triangle,
[itex]I_1=\int_o^2 xydx+2yzdy+3xzdz [/itex]
along the height of the triangle,
[itex]I_2=\int_o^2 xydx+2yzdy+3xzdz[/itex]
Now the hypoteneuse is what is getting me (I think),
I need to again evaluate [itex]\int xydx+2yzdy+3xzdz[/itex]
Are my bounds just from 0--->(2-y) ?
Casey
Homework Statement
Okay, so I have already done it using the surface integral; now I need to compute the 3 individual line integrals.
By definition, the integral (I will call it I since I am that creative) is given by:
[itex]I=\oint v\cdot\, dl[/itex]
[itex]v=<xy, 2yz, 3xz>[/itex]
[itex]dl=<dx, dy, dz>[/itex]
[itex]\Rightarrow v\dot dl=xydx+2yzdy+3xzdz[/itex]
So the three individual integrals are:
along the base of the triangle,
[itex]I_1=\int_o^2 xydx+2yzdy+3xzdz [/itex]
along the height of the triangle,
[itex]I_2=\int_o^2 xydx+2yzdy+3xzdz[/itex]
Now the hypoteneuse is what is getting me (I think),
I need to again evaluate [itex]\int xydx+2yzdy+3xzdz[/itex]
Are my bounds just from 0--->(2-y) ?
Casey