Linear Quadratic Regulator (Optimal Controller Design)

[preet]

This is a general question. When using the optimal method to design a controller, specifically a linear quadratic regulator, you usually have a state-space representation of a system, and a cost function to minimize.

The cost function usually takes the (quadratic) form:

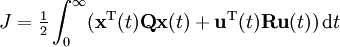
I don't understand how you choose the weight matrices Q and R to minimize or optimize your system. For example, say my single order state space system's input (u) is force, and the output (y) is speed. Further, I can make y=x, my state variable. So would a reasonable goal be to achieve minimal force and maximum speed? How do I choose Q and R to reflect this?

Also, I'm trying to tie all of this in with another method of controller design -- pole placement. I understand pole placement because I'm directly 'designing' the desired response characteristics of my system's behaviour. I don't really get optimal control in this sense. Is optimal control a 'final' step, after pole placement? Or do I use my original system and find Q and R to get desired behaviour?

 

[Valkarie]

In order to choose the weight matrices Q and R, you need to define your desired performance criteria. In this case, it is to achieve minimal force and maximum speed. You can then use the coefficients of the cost function to reflect these criteria. For example, if you want to minimize the force, you can assign a higher weight to the control input u in the cost function. Similarly, if you want to maximize the speed, you can assign a higher weight to the state variable x. This way, you can adjust the weight matrices Q and R to reflect your desired performance criteria. As for the relationship between pole placement and optimal control, they are two different methods of controller design that are used to achieve the same goal of controlling a system's behaviour. Pole placement is more direct as you are directly designing the desired response characteristics of your system by assigning the poles' position in the complex plane. On the other hand, optimal control is more general and uses a cost function to optimize the performance of your system given certain criteria. In some cases, optimal control may be used as the final step after pole placement in order to fine-tune the system's performance. In other cases, optimal control may be used as the first step to get an initial starting point for the controller before pole placement is used to further refine the controller's design.