Brydan
- 2
- 0
[Note: no template because this post was moved from the QM subforum]
I was working on problem #41 and was confused about what the wave function would look like from the time x = 0 to when E=V0. (See image in attachments)https://mail.google.com/mail/u/0/?ui=2&ik=be26b6c94d&view=fimg&th=14c66f8d9fef8e09&attid=0.1&disp=inline&realattid=1497006575826501632-local0&safe=1&attbid=ANGjdJ9_sVoeG4InQCcYyJgM9GdXq5BJUBa-YH0cv1QCny82hco_1lvkH8I3AvpB_3B_zcwK5VVtj8BIZFl_yafUAFkA85LYwtvbi40WKWRnP6ch-psjeDgoFr6Vf7k&ats=1427656728466&rm=14c66f8d9fef8e09&zw&sz=w1896-h859In class we did this problem and my professor drew something on the board that looked similar to the image below, where both the amplitude and wavelength decrease from when x = 0 to when E = V0.
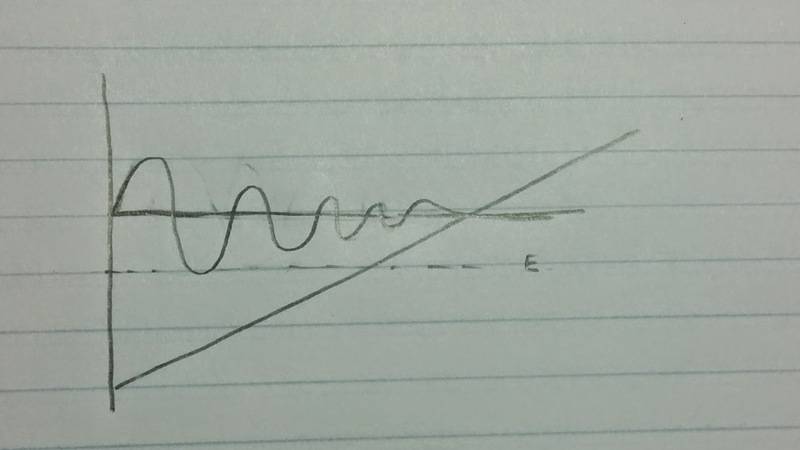
However, I don't understand this solution. as according to the equations below, the wavelength should be increasing:
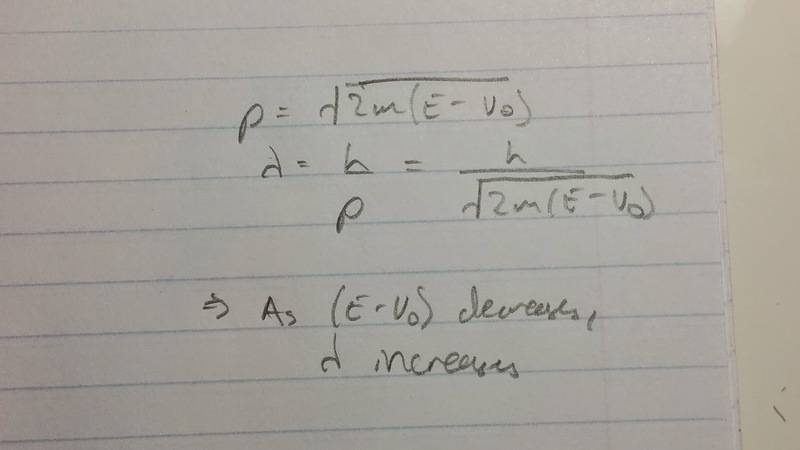 Additionally, I don't understand why the amplitude would be decreasing.
Additionally, I don't understand why the amplitude would be decreasing.
I was wondering if anyone could perhaps clarify what the amplitude and wavelength should be doing and why. My test is tomorrow so any help would be greatly appreciated. Thanks!
I was working on problem #41 and was confused about what the wave function would look like from the time x = 0 to when E=V0. (See image in attachments)https://mail.google.com/mail/u/0/?ui=2&ik=be26b6c94d&view=fimg&th=14c66f8d9fef8e09&attid=0.1&disp=inline&realattid=1497006575826501632-local0&safe=1&attbid=ANGjdJ9_sVoeG4InQCcYyJgM9GdXq5BJUBa-YH0cv1QCny82hco_1lvkH8I3AvpB_3B_zcwK5VVtj8BIZFl_yafUAFkA85LYwtvbi40WKWRnP6ch-psjeDgoFr6Vf7k&ats=1427656728466&rm=14c66f8d9fef8e09&zw&sz=w1896-h859In class we did this problem and my professor drew something on the board that looked similar to the image below, where both the amplitude and wavelength decrease from when x = 0 to when E = V0.
However, I don't understand this solution. as according to the equations below, the wavelength should be increasing:
I was wondering if anyone could perhaps clarify what the amplitude and wavelength should be doing and why. My test is tomorrow so any help would be greatly appreciated. Thanks!
Attachments
Last edited by a moderator:
