- #1
AI Thread Summary
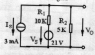
The discussion revolves around a load voltage problem where the correct answer is identified as -3. Participants highlight the importance of considering both I1 and I2 currents when calculating the final voltage across the resistor. There is an emphasis on maintaining consistent units throughout the calculations. Acknowledgment of an error in the initial approach is noted, leading to clarification on the method needed to find the fault. The conversation underscores the necessity of thorough analysis in electrical problems.
Here is what I tried
This question was actually asked in one of our engineering entrances.
The answer was 1D.
My teachers say that we have to use μₘ/fₘ to get to this answer. I cannot understand why. I'll be really glad if you could tell me the exact definition of power (numerically) that works in all scenarios.
TL;DR Summary: I would like to know the voltmeter readings on the two resistors separately in the picture in the following cases , When one of the keys is closed When both of them are opened (Knowing that the battery has negligible internal resistance)
My thoughts for the first case , one of them must be 12 volt while the other is 0
The second case we'll I think both voltmeter readings should be 12 volt since they are both parallel to the battery and they involve the key within what the...
The answer to this question is statements (ii) and (iv) are correct.
(i) This is FALSE because the speed of water in the tap is greater than speed at the water surface
(ii) I don't even understand this statement. What does the "seal" part have to do with water flowing out? Won't the water still flow out through the tap until the tank is empty whether the reservoir is sealed or not?
(iii) In my opinion, this statement would be correct. Increasing the gravitational potential energy of the...
Similar threads
Hot Threads
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math