- #1
nightshade123
- 82
- 0
[SOLVED] Loop the Loop
1. Homework Statement
A block slides on the frictionless loop the lopp track shown in this img, what is the min height at which it can start from rest and still make it around the loop
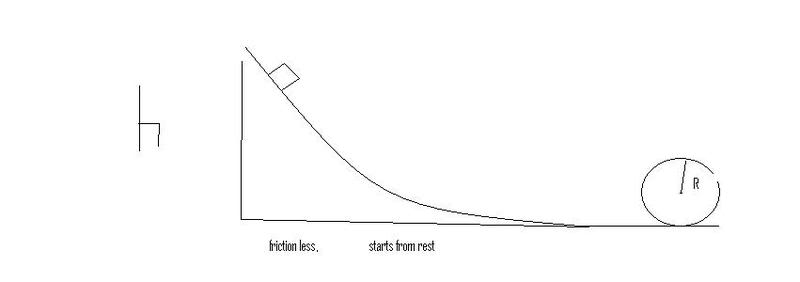
I haev solved this problem TWO ways, and i can't decide which way is correct
the eqn...
U0+K0 = K+U
where U = potential energy and K = kinetic energy
first
m * g * h + (1/2) * m * v^2 >= m * g * 2 * R
final answer = h = 2R
the way my friend set it up and solved it
m * g * h >= (1/2) * m * v^2 + m * g * 2 * R
my friend solved it this way and got h = (5*R) / 2
but i can't seem to get what he got and i get h=h-2r+2r which says the min height has to be the min height of the radius aka h = 2R
any hints, tips, or advice?
1. Homework Statement
A block slides on the frictionless loop the lopp track shown in this img, what is the min height at which it can start from rest and still make it around the loop
The Attempt at a Solution
I haev solved this problem TWO ways, and i can't decide which way is correct
the eqn...
U0+K0 = K+U
where U = potential energy and K = kinetic energy
first
m * g * h + (1/2) * m * v^2 >= m * g * 2 * R
final answer = h = 2R
the way my friend set it up and solved it
m * g * h >= (1/2) * m * v^2 + m * g * 2 * R
my friend solved it this way and got h = (5*R) / 2
but i can't seem to get what he got and i get h=h-2r+2r which says the min height has to be the min height of the radius aka h = 2R
any hints, tips, or advice?