Lubrication Theory: Fluid Flow and Integration

[E.T.A.]

Basically, I'm modelling the flow of a "coating" process -- a fluid flow between a flat moving plane and a stationary cylinder, 2D, cartesian coordinates. Subscript 0 is the at the minimum height b/w the plane and the cylinder, and subscript c is at the point at which the flow leaves the moving plane-cylinder system and into the infinite-length "coating" mechanism. Diagram below:

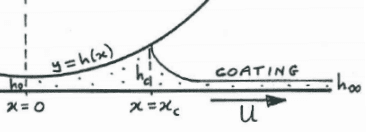
and the governing equations:

so, here's where I'm at:

• I don't really get the need for the substitution (or is it some dimensionless parameter?). It feels pretty arbitrary right now and it's frustrating.
• I have subbed in the value for h into the eq. for dp/dx, and then attempted to solve that ODE via direct integration (?), which yields something pretty nasty. And, unfortunately, I'm not quite getting at which stage the given substitution's meant to happen (or -again- why), and quite where the sins are coming from.

I'm sorry this is so long and my attempt is so weak but I'm kinda lost and I'd be madly grateful for any direction and/or help.

Thanks!

 

[Chestermiller]

This is just a straightforward trig substitution to evaluate the integrals of the terms on the right hand side of the equation with respect to x. If they wrote $x=\sqrt{2Rh_0}tan\theta$, would it make more sense to you?

Chet

 

[E.T.A.]

This is just a straightforward trig substitution to evaluate the integrals of the terms on the right hand side of the equation with respect to x. If they wrote $x=\sqrt{2Rh_0}tan\theta$, would it make more sense to you?

Chet

Yeah. Thanks, man. The answer fell out pretty easy when I stopped looking for a difficulty that wasn't there.

 

[E.T.A.]

Hey, I'm stuck again!

I'm really not sure where to start with this and I'm not ~quite~ sure where I'm meant to be working to :(

Would really appreciate any help.

 

[E.T.A.]

Don't think the image uploaded:

 

[E.T.A.]

wait: b/c γ=tan^-1 (x/sqrt (2Rh_o)), and the limit of this as x --> negative infinity will = -pi/2, thefore p (-pi/2) = 0, which would allow for the solution for the unknown c in tbe eq. for pressure (?). then, using p(γ_c)=0 the final answer can then be constructed?

this seems wrong and overly simplistic, and I have neglected the given info about the pressure grad.

help!

 

[E.T.A.]

I have actually solved this now :)

 

[E.T.A.]

hey, quick question: for this system to work, would the the height at x=0 (h_0) have to be smaller than that at h_inifinty? i.e. the pressure generation is biggest at the start of the system?

 

[Chestermiller]

hey, quick question: for this system to work, would the the height at x=0 (h_0) have to be smaller than that at h_inifinty? i.e. the pressure generation is biggest at the start of the system?

I don't fully understand this question. You are approximating the shape of the cylinder by a parabola. h_0 is the minimum clearance, so all other h values are larger. Your original equation tells you that the pressure gradient is not largest when h is large.

Chet

 

[nonotje12]

I don't fully understand this question. You are approximating the shape of the cylinder by a parabola. h_0 is the minimum clearance, so all other h values are larger. Your original equation tells you that the pressure gradient is not largest when h is large.

Chet

Apologies for replying to an old thread, but I'm doing the same task this week as OP. Do you know how y_c allows for h_c to be found?

 

[Chestermiller]

Can you please define y_c?

 

[nonotje12]

Can you please define y_c?

I don't quite know, it's one of the things I'm trying to understand. In the earlier task it states that Y_c is where the liquid separates from the surface of the cylinder. From what I also understood is that Y is an angle with lots of values but Y_c is some critical or specific value of Y.

 

[nonotje12]

I don't quite know, it's one of the things I'm trying to understand. In the earlier task it states that Y_c is where the liquid separates from the surface of the cylinder. From what I also understood is that Y is an angle with lots of values but Y_c is some critical or specific value of Y.

Wow I can see my answer now. I believe that if you have the specific angle then you should obviously know at what width the separation begins. But I can't see how I would begin to establish a continuity of flow argument to find the coating thickness.

 

[Chestermiller]

Apologies for replying to an old thread, but I'm doing the same task this week as OP. Do you know how y_c allows for h_c to be found?

Are the parameter symbols in this analysis the same as those in the OPs original post?

 

[nonotje12]

Are the parameter symbols in this analysis the same as those in the OPs original post?

Yes they are

 

[Chestermiller]

I think you should consider setting the pressure gradient from post #5 equal to the pressure gradient from post #1 (evaluated at the separation location). At least that is what I would try.

 

[nonotje12]

I think you should consider setting the pressure gradient from post #5 equal to the pressure gradient from post #1 (evaluated at the separation location). At least that is what I would try.

Here is my attempt, but I can't seem to get rid of U, (the speed of the plane surface)

 

[Chestermiller]

You are aware that $h_{\infty}=Q/U$ right?

 

[nonotje12]

You are aware that $h_{infty}=Q/U$ right?

no wasn't aware of that, can I find that somewhere?

 

[Chestermiller]

The throughput rate per unit width Q has to be equal to the velocity U times the final thickness $h_{\infty}$. That is simply conservation of mass.