Niles
- 1,834
- 0
Homework Statement
Hi
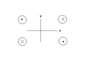
I am looking at four parallel wires of finite length L, whose currents run in the directions shown in the attached figure. There is no gradient along the wire-axis, so from Maxwell's equation
<br /> \frac{dB_x}{dx} = -\frac{dB_y}{dy} \equiv \tilde B.<br />
In order to find an expression for the gradient \tilde B given some current I, I need to use Biot-Savarts law. I think I need to make a binomial expansion for small displacements from the center, but I am not quite sure how to do this with the Biot-Savart law. I would really appreciate a hint.
Niles.