PeachBanana
- 189
- 0
Homework Statement
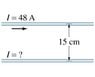
A long horizontal wire carries a current of 48 A. A second wire, made of 3.0 mm diameter copper wire and parallel to the first, is kept in suspension magnetically 15 cm below. Determine the magnitude of the current in the lower wire.
Homework Equations
μI / 2∏r
The Attempt at a Solution
B = (1.256*10^-6)(48 A) / (2∏)(.15 m)^2
B = 4.2639 * 10 ^-4 T
B(2∏r) / μ = I
(4.2639 * 10^-4 T)(2∏)(1.5*10^-3 m)/(1.256 * 10^-6)
I = 3.19 A