Magnitude of Electric field using superposition principle

[skibum143]

Homework Statement

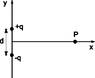
Two charges, +q and -q, are located in the x-y plane at points (0,+d/2) and (0,-d/2), respectively. Calculate the magnitude of the electric field at point P with the superposition principle.
Data: q=37.0 nanoCoulombs,
d=4.60mm and P at
x=92.0mm.

Homework Equations

E = kQ/r^2
a^2 + b^2 = c^2
sin = o/h

The Attempt at a Solution

I tried to solve this like a normal E field question.
For the +q charge, I got that the E field would be:
( k * -37E-6 (sin2) / .092^2) + ( k * 37E-6 (cos2)
and For the -q charge, I got that the E field would be:
( ( k * -37E-6 (sin2) / .092^2) - ( k * 37E-6 (cos2)
This came out to 2740 N/C (positive b/c it asks for magnitude) but that was wrong. Can someone tell me where I'm going wrong? I attached the diagram.

 

[thebigstar25]

I understood what you first did,

you first said that you will break up E= Esintheta + Ecostheta, one thing I noticed that in the equation E=kq/r^2 , you used for r = 0.092 you used the x distance for the point p, I suggest you have another look at your figure :

http://img231.imageshack.us/img231/5466/59813260.gif

compare the blue line with the red one , do you still think that the distance between q and p is x (0.092) ?

 

[skibum143]

When I did (.092^2) + (.0023^2), I get that the hypotenuse is .0092...

 

[skibum143]

Ah, sorry my mistake, I now get .00847. I will try that. Was the rest of the setup ok? Thanks for your help!

 

[skibum143]

Hmmm... that was still wrong. Am I doing something else incorrectly?

 

[thebigstar25]

i think the required distance between q and p should be sqrt((0.092^2) + (0.0023^2)) i did the calculation and i got 0.092028 (when you said it is 0.00847 you didnt take the square root) ..

another thing, I think you probably haven't considered the elecrtic field produced from positive charge and negative charge, have a look at this figure:

http://img402.imageshack.us/img402/7681/95152182.jpg

so your problem should look something like the following:

http://img4.imageshack.us/img4/4996/34194234.gif

notice where r the electric field vectors , find the components of each vectors ,then see whether you will find any compenents that will cancel with each other and pay attention to the directions ..

by the way , i have one question for you , from where you get sin2 and cos2?