zenterix
- 774
- 84
- Homework Statement
- I would like to go through the sequence of ideas presented in the notes I am reading about electromagnetism.
The notes are about Faraday's law.
The sequence of examples and concepts seems a bit scattered to me.
- Relevant Equations
- It seems to me I understand the scenarios presented below individually, but when I consider them together it doesn't seem to fit perfectly.
For example, in scenario 1 the notes talk about potential difference in a conducting bar as being the emf.
Then in scenario 3, the notes say that the concept of potential difference is no longer well-defined for a non-electrostatic electric field.
In addition, in scenario 1, emf is "the work done by the magnetic force per unit charge". But don't magnetic forces operate orthogonally to velocity and thus displacement?
My goal with this post is to write out the ideas and perhaps someone can fill in the confusing parts for me.
Scenario 1
Consider a conducting bar of length ##l## moving through a uniform magnetic field as depicted below
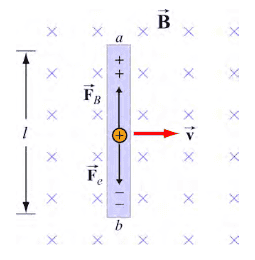
1. Particles with charge ##q## inside experience a magnetic force ##\vec{F}_B=q\vec{v}\times\vec{B}## that pushes them upward, leaving negative charge on the lower end.
2. An electric field ##\vec{E}## arises inside the bar producing a downward electric force ##\vec{F}_e=q\vec{E}##.
3. At equilibrium, the two forces cancel
$$|\vec{F}_B|=qvB=qE=|\vec{F}_e|$$
$$E=vB$$
4. The potential difference between the two ends of the conductor is
$$V_{ab}=V_a-V_b=\mathcal{E}=El=vBl$$
This potential difference is called the motional electromotive force (motional emf).
Now, there is no loop here, so I am not sure what magnetic flux means here.
Scenario 2
Next consider that the conducting bar slides along two frictionless conducting rails that are at a distance ##w## apart and connected together by a resistor with resistance ##R##.
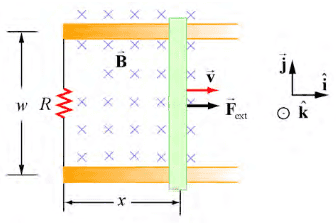
Then the emf is defined
$$\mathcal{E}=\oint \frac{\vec{F}_B}{q}\cdot d\vec{s}=\oint_{loop} (\vec{v}\times\vec{B})\cdot d\vec{s}$$
$$=\int_{bar}vB\hat{j}\cdot (dy\hat{j})=Bwv$$
Note that in this case the induced current can be explained by the magnetic force on the charges in the conductor due to the relative motion between the loop and the magnetic field.
This last statement is a bit confusing to me since I was under the impression that magnetic fields don't do work.
Scenario 3
Next consider a stationary closed conducting path (e.g. a coil) as below.
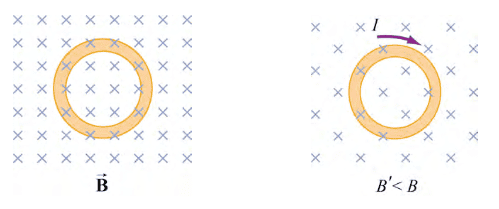
If we decrease the magnetic flux through the loop by decreasing the strength of the magnetic field then experimentally, while the magnetic field is changing, a current is observed in the loop in the clockwise direction.
Faraday conjectured that this phenomenon is due to a non-electrostatic electric field.
$$\mathcal{E}=\oint \vec{E}\cdot d\vec{s}$$
The electric field cannot be electrostatic because the line integral of such a field must vanish.
$$\oint\vec{E}\cdot d\vec{s}=-\frac{d\Phi_B}{dt}$$
The concept of potential difference is not well-defined any longer for such a non-electrostatic electric field.
The source of this electric field is the magnetic field changing with time.
The force on a charge is ##\vec{F}_{e}=q\vec{E}## and the emf is defined
$$\mathcal{E}=\oint_{loop}\frac{\vec{F}_e}{q}\cdot d\vec{s}=\oint_{loop}\vec{E}\cdot d\vec{s}$$
This closed loop line integral can be non-zero. This is a different electric field from the electric field produced by static charges, which was conservative.
Finally, Faraday's law says that a time-varying magnetic flux is the source of a non-conservative electric field
$$\mathcal{E}=\oint_{loop}\vec{E}\cdot d\vec{s}=-\frac{d\Phi_{mag}}{dt}$$
Consider a conducting bar of length ##l## moving through a uniform magnetic field as depicted below
1. Particles with charge ##q## inside experience a magnetic force ##\vec{F}_B=q\vec{v}\times\vec{B}## that pushes them upward, leaving negative charge on the lower end.
2. An electric field ##\vec{E}## arises inside the bar producing a downward electric force ##\vec{F}_e=q\vec{E}##.
3. At equilibrium, the two forces cancel
$$|\vec{F}_B|=qvB=qE=|\vec{F}_e|$$
$$E=vB$$
4. The potential difference between the two ends of the conductor is
$$V_{ab}=V_a-V_b=\mathcal{E}=El=vBl$$
This potential difference is called the motional electromotive force (motional emf).
Now, there is no loop here, so I am not sure what magnetic flux means here.
Scenario 2
Next consider that the conducting bar slides along two frictionless conducting rails that are at a distance ##w## apart and connected together by a resistor with resistance ##R##.
Then the emf is defined
$$\mathcal{E}=\oint \frac{\vec{F}_B}{q}\cdot d\vec{s}=\oint_{loop} (\vec{v}\times\vec{B})\cdot d\vec{s}$$
$$=\int_{bar}vB\hat{j}\cdot (dy\hat{j})=Bwv$$
Note that in this case the induced current can be explained by the magnetic force on the charges in the conductor due to the relative motion between the loop and the magnetic field.
The emf is the work done by the magnetic force per unit charge.
This last statement is a bit confusing to me since I was under the impression that magnetic fields don't do work.
Scenario 3
Next consider a stationary closed conducting path (e.g. a coil) as below.
If we decrease the magnetic flux through the loop by decreasing the strength of the magnetic field then experimentally, while the magnetic field is changing, a current is observed in the loop in the clockwise direction.
Faraday conjectured that this phenomenon is due to a non-electrostatic electric field.
$$\mathcal{E}=\oint \vec{E}\cdot d\vec{s}$$
The electric field cannot be electrostatic because the line integral of such a field must vanish.
$$\oint\vec{E}\cdot d\vec{s}=-\frac{d\Phi_B}{dt}$$
The concept of potential difference is not well-defined any longer for such a non-electrostatic electric field.
The source of this electric field is the magnetic field changing with time.
The force on a charge is ##\vec{F}_{e}=q\vec{E}## and the emf is defined
$$\mathcal{E}=\oint_{loop}\frac{\vec{F}_e}{q}\cdot d\vec{s}=\oint_{loop}\vec{E}\cdot d\vec{s}$$
This closed loop line integral can be non-zero. This is a different electric field from the electric field produced by static charges, which was conservative.
Finally, Faraday's law says that a time-varying magnetic flux is the source of a non-conservative electric field
$$\mathcal{E}=\oint_{loop}\vec{E}\cdot d\vec{s}=-\frac{d\Phi_{mag}}{dt}$$