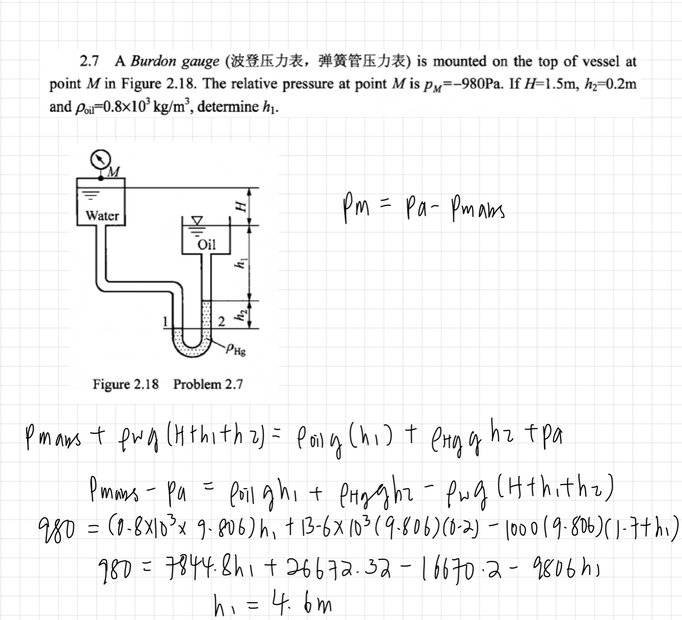
SUMMARY
The correct calculation for determining height from relative pressure using a manometer yields a result of 5.6 meters. The formula used is PM abs = Patm + PM, which indicates that the absolute pressure is the sum of atmospheric pressure and gauge pressure. The initial confusion arose from the incorrect application of the formula PM gauge = Patm - PM abs. This highlights the importance of correctly identifying the type of pressure being measured.
PREREQUISITES
- Understanding of fluid mechanics principles
- Familiarity with pressure measurement concepts
- Knowledge of manometer types and their applications
- Basic algebra for manipulating pressure equations
NEXT STEPS
- Study the principles of hydrostatic pressure in fluids
- Learn about different types of manometers and their uses
- Explore the derivation of pressure equations in fluid mechanics
- Investigate the effects of atmospheric pressure variations on measurements
USEFUL FOR
Students and professionals in engineering, physics, and any field requiring precise pressure measurements and fluid dynamics understanding.