Mass and pulley system question

[Dtbennett]

Homework Statement

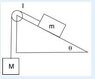
A mass M = 53 g hangs from a light, inextensible string. It passes without sliding over a pulley. The pulley can be treated as a solid homogeneous disc with mass mp = 12 g and radius 3.6 cm, that turns without friction on its axis. The other end is attached to a mass m = 27 g that slides without friction on a plane inclined at angle θ = 25° to the horizontal. What is the acceleration of mass M?

Homework Equations

I of disk = 1/2MR^2

The Attempt at a Solution

Okay, so I am attempting to find the acceleration of the mass downwards. Due to Newton's second law, the sum of all forces is 0. Therefore logically, the acceleration should be

acceleration of M = Mg - (inertia of disk + mgsin(x) )

so acceleration of M = 0.054x9.8 - [(0.5 x 0.012 x 3.6^2) + (0.027x 9.8 x sin25)]

But for some reason I am not getting the right answer. Am I approaching it incorrectly?

 

[haruspex]

You are mixing up several different kinds of physical entity. You are subtracting a moment of inertia from a force and taking the answer to be an acceleration. You can only add or subtract or equate two things if they have the same dimensionality - both forces, both accelerations, both moments of inertia, etc.

Best is to consider each mass separately, creating extra symbols for unknowns as necessary. What are the forces acting on the suspended mass? Write down the ∑F= ma equation for that. Then do the same for the pulley (∑torque = Iα in this case) and again for the other mass.
Be careful wrt the tensions in the string. The tension one side of the pulley will be different from that on the other side.