ikihi
- 81
- 2
Homework Statement
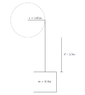
Consider a pulley with a mass-less cord attached to its edge. The rope hangs a distance of d= 2.50 m below the bottom of the pulley. Attached to the end of this cord is a block with mass 3.00 kg. There is also an electric motor attached to the pulley which supplies a torque of 28.7 N * m. The pulley can be considered a disk with a radius of 0.65 m. The mass of the pulley is 1.3 kg.
a) What is the torque due to the hanging block? Answer: 19.11 N ⋅ m
b) what is the moment of inertia of the pulley? Answer: 0.2746 kg ⋅ m
c) Once the motor is turned on the pulley begins to rotate counter clock-wise. What is the magnitude of the angular acceleration of the pulley? Answer: 6.22 rad/sec2
d) Through how many radians must the pulley rotate in order to lift the block to the bottom edge of the pulley?
e) Once the motor is turned on, how long will it take the top edge of the block to reach the bottom of the pulley?
Homework Equations
I = 0.5 * m * r^2 (moment of inertia)
The Attempt at a Solution
I need help with d and e.
[/B]
d) The circumference of the pulley is 4.08 m and the cord is 2.50 m. So the total rotation length is 1.58 m. How do i find how many revolutions from this? It should be less than 1 revolution, correct?
e) t = ± √(2⋅θ)/(α)
t = ?