Massive rotating drum on bearings with friction

Click For Summary

Discussion Overview

The discussion revolves around a physics problem involving a massive rotating drum mounted on bearings, focusing on the forces at play, particularly the friction between the drum and the bearings. Participants are exploring the dynamics of the system, including torque, force couples, and the implications of friction on the motion of the drum.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant describes a system where a mass m' is suspended from a rope wound around a drum of mass m, raising questions about the forces acting on the drum and the resulting friction at the bearings.
  • The same participant proposes that the force couple created by the tensions in the rope contributes to the torque and affects the normal force on the bearings, potentially increasing friction.
  • Another participant questions the nature of the friction, seeking clarification on what surfaces are in contact and how forces are balanced in the system.
  • A later reply clarifies that the friction discussed is between the inner hole of the drum and the bearings, indicating a more specific focus on the interaction at that interface.
  • One participant suggests a different approach by recommending the drawing of the friction force in a specific direction and introducing variables for angular acceleration to solve the problem.

Areas of Agreement / Disagreement

Participants express differing views on the role of friction and the forces involved, with no consensus reached on the correct approach to analyzing the system. The discussion remains unresolved regarding the implications of the forces and the correct method to calculate friction.

Contextual Notes

There are limitations in the initial descriptions, including assumptions about the forces acting on the drum and the nature of the friction. The discussion also reflects a dependency on the definitions of the forces involved and the geometry of the system.

erore
Messages
5
Reaction score
0
I came across the following example. I have a mass m' that is suspended from a massless rope which is wound around a drum of mass m. The radius of the drum is R. The drum is fixed on a shaft with bearings of radius r. I am supposed to determine coefficient of friction between the bearings and the drum but for now I am stuck with the forces diagram.
I created something like that:
attachment.php?attachmentid=51334&stc=1&d=1349007090.gif


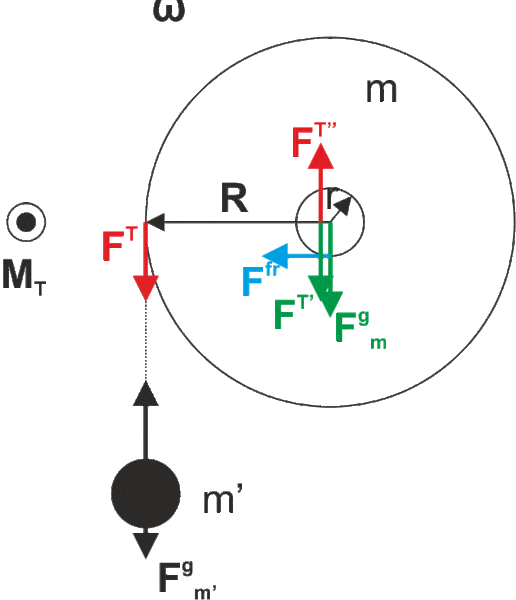
In my solution I add a pair of forces of the same magnitude and opposite direction F^{T''} and F^{T'}. F^{T''} and F^{T} make a force couple which generates some momentum about the axis of the drum (which contributes to rotation motion). However, F^{T'} acts on the center of mass of the drum and adds up with gravitation force. Thus, the resulting force exerted by the drum on the bearing is bigger than if there was no m'. Consequently the friction is bigger too.

My question is whether this is correct. The solution I have only calculates the torque due to m' and does not introduce the force couple therefore it does not have the additional force on the center of mass and consequentially no additional item in the normal force and friction respectively.

I am also curious, the friction itself produces a torque, if my reasoning above is correct, it would create another force couple, giving rise yet to another force acting on the center of mass of the drum which could go on and on. This is confusing for me at the moment.
 

Attachments

  • drum.gif
    drum.gif
    12.4 KB · Views: 1,048
Last edited:
Physics news on Phys.org
Friction between what and what? Is the drum attached to something or in contact with something? That will somehow balance the force FT (otherwise the whole setup accelerates downwards).
 
I am sorry, the first paragraph was nonsense. I corrected. Basically, there is a hole in the middle of the drum of radius r and a shaft with bearings is inserted into that hole. The friction I mention is between the inner hole of the drum and the bearings.
 
Ah. I think I would draw the friction force at the upper side and in the other direction.
Afterwards, I would add variables for the angular acceleration and the force on the shaft and solve for those.
 

Similar threads

High School Calculating the torque needed to rotate a drum
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Calculate Force Applied to Rope for Frictional Torque
  • · Replies 2 ·
Replies
2
Views
5K
High School Static friction needed for rolling without slipping
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad Rolling Without Slipping
  • · Replies 59 ·
2
Replies
59
Views
5K
Undergrad Torque required from powered roller to rotate cylinder
  • · Replies 19 ·
Replies
19
Views
3K
MIT 8.01: Unwinding Drum Problem
  • · Replies 9 ·
Replies
9
Views
3K
Graduate Trying to understand couple stress in continua
  • · Replies 6 ·
Replies
6
Views
1K
Graduate Boundary condition of limiting friction in continuum mechanics
  • · Replies 18 ·
Replies
18
Views
2K
Motor Sizing for Wheel Endurance Testing
  • · Replies 4 ·
Replies
4
Views
2K
Graduate Predicting Peak Displacement in Imbalanced Rotating Drum
  • · Replies 35 ·
2
Replies
35
Views
5K