hieule
- 5
- 0
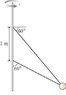
Two wires are tied to the 2.0 kg sphere shown in the figure View Figure . The sphere revolves in a horizontal circle at constant speed.
For what speed is the tension the same in both wires?
What is the tension?
I reallllly need some hints to figure the first part, and the second part...thank you
For what speed is the tension the same in both wires?
What is the tension?
I reallllly need some hints to figure the first part, and the second part...thank you