Matching interaction terms and decay processes in standard model

[spaghetti3451]

I would like to consider the interaction terms in the Standard Model which allow the following decay process:

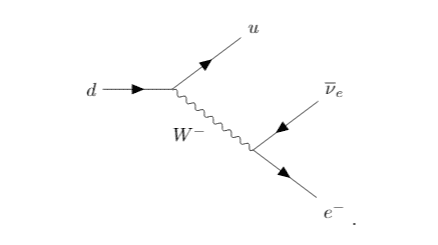
The only interaction terms in the Standard Model which allow this decay process are contained in the charged current interactions:

$$\mathcal{L}_{cc}
= ie_{W}\big[W_{\mu}^{+}(\bar{\nu}'_{m}\gamma^{\mu}(1+\gamma_{5})e'_{m} + V_{mn}\bar{u}'_{m}\gamma^{\mu}(1+\gamma_{5})d'_{n})
+ W_{\mu}^{-}(\bar{e}'_{m}\gamma^{\mu}(1+\gamma_{5})\nu'_{m} + (V^{\dagger})_{mn}\bar{d}'_{m}\gamma^{\mu}(1+\gamma_{5})u'_{n})\big].$$

-----------------------------------------------------------------------------------------------------------------------------------

1. Is the vertex between the quarks only allowed by the term $ie_{W}W_{\mu}^{+} V_{mn}\bar{u}'_{m}\gamma^{\mu}(1+\gamma_{5})d'_{n}$?

2. Is this because the down quark enters the vertex and therefore must not have a bar on top of it?

3. Simialrly, is the vertex between the leptons only allowed by the term $ie_{W}W_{\mu}^{-} (V^{\dagger})_{mn}\bar{d}'_{m}\gamma^{\mu}(1+\gamma_{5})u'_{n}$?

 

[Orodruin]

You are missing minus signs in your projection operators. CC iteractions act on left-handed fields only.

1,2) Yes.

3) No, you need the lepton fields in the operator.

 

[spaghetti3451]

You are missing minus signs in your projection operators. CC iteractions act on left-handed fields only.

But the left-handed projection operator has a plus sign in the mostly positive metric, does it not? I'm using Cliff Burgess's textbook, although I should be using mostly negative because it is the common usage in the particle physics community.

3) No, you need the lepton fields in the operator.

Right, my bad.