- #1
- 18,994
- 23,995
Questions
2. Show that the dihedral group ##D_{12}## of order twelve is the finite reflection group of the root system of type ##G_2##.
3. (solved by @Periwinkle ) Consider the set
$$
\mathcal{P}_n := \{\,\{2\},\{4\},\ldots,\{2n\}\,\} \subseteq \mathcal{P}(\mathbb{N})
$$
4. (solved by @Periwinkle ) Linear Operators. (Only solutions to both count!)
m = \inf_{t\in [0,1]} g(t)\; , \;M = \sup_{t\in [0,1]} g(t)
$$
(x,\alpha +\beta ) = (x,\alpha)(y,\beta) + (x,\beta)(y,\alpha)
$$
7. (solved by @Periwinkle ) Prove that for all ##a,b,c \in \mathbb{R}## holds $$a>0\wedge b>0\wedge c>0 \Longleftrightarrow a+b+c>0\wedge ab+ac+bc>0\wedge abc>0\,.$$
8. (solved by @Periwinkle ) Let ##a,b \in L^2\left( \left[ -\frac{\pi}{2},+\frac{\pi}{2} \right] \right)## given as
$$
a(x)=11\sin(x) + 8\cos(x) \; , \;b(x)=4\sin(x) + 13\cos(x)
$$
9. (solved by @Couchyam) Let ##\varepsilon_k :=\begin{cases}1&,\text{ if the decimal representation of }k\text{ has no digit }9\\0&, \text{ otherwise }\end{cases}##
\xi(x) \in (\min\{x,x_0\},\max\{x,x_0\})
$$

1. a. Let ##(\mathfrak{su}(2,\mathbb{C}),\varphi,V)## be a finite dimensional representation of the Lie algebra ##\mathfrak{g}=\mathfrak{su}(2,\mathbb{C})##.Calculate ##H\,^0(\mathfrak{g},\varphi)## and ##H\,^1(\mathfrak{g},\varphi)## for the Chevalley-Eilenberg complex in the cases
(i) ##(\varphi,V)= (\operatorname{ad},\mathfrak{g})##
(ii) ##(\varphi,V)= (0,\mathfrak{g})##
(iii) ##(\varphi,V)= (\pi,\mathbb{C}^2)## is the natural representation on ##\mathbb{C}^2##.
b. Consider the Heisenberg algebra ##\mathfrak{g}=\mathfrak{h}=\left\{ \left.\begin{pmatrix}0&a&c\\0&0&b\\0&0&0\end{pmatrix}\right|a,b,c\in \mathbb{R}\right\}## and calculate ##H\,^0(\mathfrak{h},\operatorname{ad})## and ##H\,^1(\mathfrak{h},\operatorname{ad})\,.##
2. Show that the dihedral group ##D_{12}## of order twelve is the finite reflection group of the root system of type ##G_2##.
3. (solved by @Periwinkle ) Consider the set
$$
\mathcal{P}_n := \{\,\{2\},\{4\},\ldots,\{2n\}\,\} \subseteq \mathcal{P}(\mathbb{N})
$$
and determine the ##\sigma-##algebra ##\mathcal{A}_\sigma(\mathcal{P}_n) \subseteq \mathcal{P}(\mathbb{N})##, and show that ##\bigcup_{n\in \mathbb{N}}\mathcal{A}_\sigma(\mathcal{P}_n)## isn't a ##\sigma-##algebra.
4. (solved by @Periwinkle ) Linear Operators. (Only solutions to both count!)
a. Show that eigenvectors to different eigenvalues of a self-adjoint linear operator are orthogonal and the eigenvalues real.
b. Given a real valued, bounded, continuous function ##g \in C([0,1])## with
$$m = \inf_{t\in [0,1]} g(t)\; , \;M = \sup_{t\in [0,1]} g(t)
$$
and an operator ##T_g(f)(t):= g(t)f(t)## on the Hilbert space ##\mathcal{H}=L^2([0,1])\,.##
Calculate the spectrum of ##T_g\,.##
5. Let ##\mathbb{F}## be a field. Then for a polynomial ##f \in \mathbb{F}[X_1,\ldots,X_n]## we define ##D(f)=\{\,q\in \mathbb{A}^n(\mathbb{F})\,|\,f(q)\neq 0\,\}##.Show that these sets build a basis of the Zariski topology on ##\mathbb{A}^n(\mathbb{F})##, and decide whether finitely many of them are sufficient to cover a given open set.
6. Let ##R := \mathbb{Q}[x,y]/\langle x^2+y^2-1 \rangle## and ##\varphi \in \operatorname{Der}(R)## a ##\mathbb{Q}-##linear derivation such that ##\varphi(x)=y\; , \;\varphi(y)=-x\,.##A derivation ##\varphi\, : \,R \longrightarrow R ## of an algebra ##R## is a linear function with ##\varphi(p\cdot q)=\varphi(p)\cdot q + p\cdot \varphi(q)\,.##
a. Determine the kernel of ##\varphi\,.##
b. Solve ##\varphi^2 + \operatorname{id} = 0\,.##
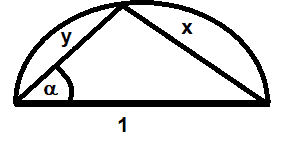
c. Since ##x^2+y^2=1## we can apply Thales' theorem and identify ##(x,\alpha),(y,\alpha)## with the sides of a right triangle with hypotenuse (diameter) ##1## according to an angle ##\alpha\,.##
Show that
$$(x,\alpha +\beta ) = (x,\alpha)(y,\beta) + (x,\beta)(y,\alpha)
$$
7. (solved by @Periwinkle ) Prove that for all ##a,b,c \in \mathbb{R}## holds $$a>0\wedge b>0\wedge c>0 \Longleftrightarrow a+b+c>0\wedge ab+ac+bc>0\wedge abc>0\,.$$
8. (solved by @Periwinkle ) Let ##a,b \in L^2\left( \left[ -\frac{\pi}{2},+\frac{\pi}{2} \right] \right)## given as
$$
a(x)=11\sin(x) + 8\cos(x) \; , \;b(x)=4\sin(x) + 13\cos(x)
$$
Calculate the angle ##\varphi = \sphericalangle (a,b)## between the two vectors.
9. (solved by @Couchyam) Let ##\varepsilon_k :=\begin{cases}1&,\text{ if the decimal representation of }k\text{ has no digit }9\\0&, \text{ otherwise }\end{cases}##
Show that ##\sum_{k=1}^\infty \dfrac{\varepsilon_k}{k}## converges.
10. (solved by @Periwinkle ) Let ##x_0\in [a,b]\subseteq \mathbb{R}## and ##f\, : \,[a,b]\longrightarrow \mathbb{R}## continuous and differentiable on ##[a,b]-\{x_0\}##.Furthermore exists the limit ##c:=\lim_{x \to x_0}f\,'(x)\,.## Then ##f(x)## is differentiable in ##x_0## with ##f\,'(x_0)=c\,.##
Proof: Let ##x\in [a,b]-\{x_0\}##. According to the mean value theorem for differentiable functions there is a
$$\xi(x) \in (\min\{x,x_0\},\max\{x,x_0\})
$$
with ##f\,'(\xi(x))=\dfrac{f(x)-f(x_0)}{x-x_0}\,.## Because ##\lim_{x \to x_0}\min\{x,x_0\}=\lim_{x \to x_0}\max\{x,x_0\}=x_0## we must have ##\lim_{x \to x_0}\xi(x)=x_0## and by assumption ##\lim_{x \to x_0}f\,'(\xi(x))=c##, hence ##\lim_{x \to x_0}\dfrac{f(x)-f(x_0)}{x-x_0}=c##.
What has to be regarded in this proof, and is there a way to avoid this hidden assumption?
11. A house ##H## and a rosary ##R## are near a circular lake ##L##.
The Gardener walks with two watering cans from the house to the lake, fills the cans and goes to the rosary. We assume ##\overline{HR}\cap L=\emptyset##.
At which point ##S## of the shore does he have to get water, so that his path length is minimal, and why?
12. How long is the distance on a direct flight from London to Los Angeles and where is its most northern point?
How long will it last by an assumed average speed of ##494## knots over ground? We neglect the influence of weather, esp. wind.
We take the values ##51°\,28'\,39''\,N,\,0°\,27'\,41''\,W## for LHR in London,
##\,33°\, 56'\,33''\,N,\,118°\,24'\,29''\,W## for LAX in Los Angeles, and a radius of ##3,958## miles for earth.
13. Trial before an American district court.
The witness claims he saw a blue cab drive off after a night accident. The judge decides to test the reliability of the witness.
Result: The witness recognizes the color correctly in the dark in ##80\%## of all cases.
A survey also found that ##85\%## of taxis in the city are green and ##15\%## are blue.
With which probability has the taxi actually been blue?
14. A monk climbs a mountain.
He starts at ##8\,##a.m. on ##1000\,##m above sea level and reaches the peak at ##8\,##p.m. at ##3000\,##m.
After a bivouac on top of the mountain, he returns to the valley the next morning and again starts at ##8\,##a.m. and returns at ##8\,##a.m.
a. If he wants to avoid being at the same time of day at the same place as the day before when he climbed upwards, which strategy must he use downwards, and why?
b. Assume he climbed at a rate of height ##u(t)## proportional to the square root of time, determine his path dependent on hourly noted time ##t##.
c. Assume he follows the same path downwards and the height of his path is given by ##d_1(t)= \dfrac{125}{9}(t-20)^2+1000## in the first three hours and ##d_2(t)=-125\,t+3500## for the rest of his way. When will he be at the same point as the day before and at which height.
15. I'm annoyed by my two new alarm clocks. They both are powered by the grid.
One leaps two minutes an hour and the other one runs a minute an hour too fast. Yesterday I took the effort and set them to the correct time. This morning, I assume there was a power loss, one clock showed exactly ##6\,a.m## while the other one showed ##7\,a.m.##
When did I set the clocks and how long did they run?
Last edited: