tmiddlet
- 26
- 0
This is not a homework/coursework problem, but I came across it and wanted to check my answer.
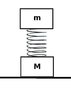
As in the diagram, there are two blocks of mass M and m. The mass m is suspended above M by a spring of spring constant k.
Initially, the block m is pushed down with a force 3mg until the system reaches equilibrium, then the force is released.
What is the maximum value for M for which the bottom block will jump off the ground?
F = kx
F = mg
U = \frac{1}{2}kx^2
I think this is the right way to do it, but I'm not sure.
To find the equilibrium offset:
3mg = kx
x = \frac{3mg}{k}
Finding the potential energy due to the spring:
\frac{1}{2}kx^2 = \frac{9m^2g^2}{2k}
To find the maximum upward offset (d) of the spring after release:
\int_{-3mg/k}^{d} (-kx-mg)dx = -\frac{9m^2g^2}{2k}
Evaluating this returns : (If I did it right)
d = \frac{mg(\sqrt{7}-1)}{k}
If kx > Mg, then the block will lift off, so I end up with:
M \lt m(\sqrt{7}-1)
I'm just curious if I got this right. If anybody is willing to try the problem or check my logic, that would be great. Thank you!
Homework Statement
As in the diagram, there are two blocks of mass M and m. The mass m is suspended above M by a spring of spring constant k.
Initially, the block m is pushed down with a force 3mg until the system reaches equilibrium, then the force is released.
What is the maximum value for M for which the bottom block will jump off the ground?
Homework Equations
F = kx
F = mg
U = \frac{1}{2}kx^2
The Attempt at a Solution
I think this is the right way to do it, but I'm not sure.
To find the equilibrium offset:
3mg = kx
x = \frac{3mg}{k}
Finding the potential energy due to the spring:
\frac{1}{2}kx^2 = \frac{9m^2g^2}{2k}
To find the maximum upward offset (d) of the spring after release:
\int_{-3mg/k}^{d} (-kx-mg)dx = -\frac{9m^2g^2}{2k}
Evaluating this returns : (If I did it right)
d = \frac{mg(\sqrt{7}-1)}{k}
If kx > Mg, then the block will lift off, so I end up with:
M \lt m(\sqrt{7}-1)
I'm just curious if I got this right. If anybody is willing to try the problem or check my logic, that would be great. Thank you!