Mesh Current Analysis: Solve & Determine Magnitudes/Voltages

[orangeincup]

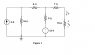
Homework Statement

Solve using the Mesh-current method. Determine the current magnitudes and the voltages across all elements

Homework Equations

i=v/r
i1+i2+i3..=0

The Attempt at a Solution

loop 1:
16(i3-3)+25i1-5i2=12
loop2:
4i1-5i2=15

1) i1=5/9i2-1

substituting 1) into loop2 gives
-25/9i2+5+16i2=-12
i2=1.1344

substituting i2=1.1233 into 1) gives i1=4.672

Can someone show me where I'm going wrong? I think I messed up the signs somewhere, I tried it a few ways and can't get it to satisfy KCL after I check my answer.

 

[Hesch]

Can someone show me where I'm going wrong? I think I messed up the signs somewhere

That's impossible, because you have not sketched any loops or any currents ( except for i₀ ).

You are the one to decide positive directions, etc.

 

[orangeincup]

My i1 is the middle loop (clockwise direction) and my i2 is the right loop (counter clockwise direction)
My i3 is the far left loop (clockwise direction) and the current was given as 3A

 

[gneill]

My i1 is the middle loop (clockwise direction) and my i2 is the right loop (counter clockwise direction)
My i3 is the far left loop (clockwise direction) and the current was given as 3A

loop 1:
16(i3-3)+25i1-5i2=12
loop2:
4i1-5i2=15

Given the above I don't see how you arrived at your two loop equations. If i3 has a given value, why does the i3 variable appear in the Loop1 equation? Loop 2 has a total of 16 Ohms in it, yet I don't see where your equation accounts for i2 flowing through that, nor how i1 is flowing through 4 Ohms for that loop when I see that a 5 Ohm resistor borders the loops.

I think you need to redo your loop equations. In general it's usually beneficial to choose the same loop direction for all loops (one reason has to do with some really handy and time saving matrix solving methods that you'll learn about soon) Here's a diagram to help:

I suggest that as a first step you might eliminate the 3 A mesh by moving its effect into the i1 loop as a fixed voltage source (due to its flowing through the 16 Ohm resistor).

 

[Hesch]

@orangeincup

I suggest that as a first step you might eliminate the 3 A mesh by moving its effect into the i1 loop as a fixed voltage source

Your i₃ = 3A, simply because i₃ is the only loop-current that passes the current-source.

As for i₂-loop you will get ( according to figure in #4 ):

+12V - ( 5 + 1 + 10 )Ω * i2 - 5Ω( -i₁ ) = 0 ( i₁ has opposite direction as to i₂ )

And the equation as for i₁?

Now, solve the 3 equations ( your calculator can probably do that simultaniously), or substitute i₃ = 3A ( leaving 2 equations ).

i_16Ω upward = i₁ - i₃ and so on.

Calculate the voltages by ohm's law.