SparkimusPrime
- 35
- 0
A group of physics students designed the following experiment to test the model of conservation of charge.
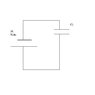
a) They first charged a capacitor C1 = 5600 micro F by applying a voltage V_0 = 10 volts (as shown in attachment Exam 2 - Problem 2 - Part a.JPG)
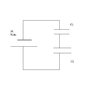
b) Then the connected a second capacitor of C2 = 1400 micro F in the circuit (as shown in Exam 2 - Problem 2 - Part b.JPG). They measured the voltage across C1 using a voltmeter. The reading of V_1 = 2 volts.
c) Then they calculated charge q_0 in the capacitor C1 in the circuit in part a and charges q_1 and q_2 in part b. Finally, they tried to compare the value of q_0 with the value of q_1 + q_2. They concluded that charge is conserved if q_0 = q_1 + q_2. Otherwise charge is not conserved.
The correct answer is supposed to be that all the charges are equal (q_0 = q_1 = q_2). But I get answers agreeing with the assessment of the experiment:
q_0 = C1 * V_0 = (10) * (5600) = 5.6e4 micro C
As shown in the figure, the total capacitance of the system decreases, because the capacitors are placed in series:
1 / C_total = 1 / C_1 + 1 / C_2
C_total = 1120 micro F
So the charge on the system should be decreased similarly (as the electric force between the plates decreases so too should the charge on the individual capacitors and thus the system). So it seems to me, by inspection that there should by such a relationship as expressed in the experiment.
If the voltage across C1 (in part b) is 2 volts, the charge on that capacitor should be:
C1 * V_1 = (5600)*(2) = 11200 micro C
Clearly less than the original charge. Of course this may be where my error occurs, I'm taking the charge across a single capacitor in a series, can I treat it as if it were alone or do I have to consider the entire system?
Also as an aside, I don't think the LaTeX system is working correctly. I tried to denote some Greek symbols (mu and delta) via latex and it showed some very strange behavior:
Edit:
Apparently I can't attach more than one image, nor can I attach an image after I've removed it. I'll reply to this thread with the appropriate images.
a) They first charged a capacitor C1 = 5600 micro F by applying a voltage V_0 = 10 volts (as shown in attachment Exam 2 - Problem 2 - Part a.JPG)
b) Then the connected a second capacitor of C2 = 1400 micro F in the circuit (as shown in Exam 2 - Problem 2 - Part b.JPG). They measured the voltage across C1 using a voltmeter. The reading of V_1 = 2 volts.
c) Then they calculated charge q_0 in the capacitor C1 in the circuit in part a and charges q_1 and q_2 in part b. Finally, they tried to compare the value of q_0 with the value of q_1 + q_2. They concluded that charge is conserved if q_0 = q_1 + q_2. Otherwise charge is not conserved.
The correct answer is supposed to be that all the charges are equal (q_0 = q_1 = q_2). But I get answers agreeing with the assessment of the experiment:
q_0 = C1 * V_0 = (10) * (5600) = 5.6e4 micro C
As shown in the figure, the total capacitance of the system decreases, because the capacitors are placed in series:
1 / C_total = 1 / C_1 + 1 / C_2
C_total = 1120 micro F
So the charge on the system should be decreased similarly (as the electric force between the plates decreases so too should the charge on the individual capacitors and thus the system). So it seems to me, by inspection that there should by such a relationship as expressed in the experiment.
If the voltage across C1 (in part b) is 2 volts, the charge on that capacitor should be:
C1 * V_1 = (5600)*(2) = 11200 micro C
Clearly less than the original charge. Of course this may be where my error occurs, I'm taking the charge across a single capacitor in a series, can I treat it as if it were alone or do I have to consider the entire system?
Also as an aside, I don't think the LaTeX system is working correctly. I tried to denote some Greek symbols (mu and delta) via latex and it showed some very strange behavior:
\mu
This would work correctly as long as it was at the top of the post.
\Delta
This would work correctly as long as there was another latex symbol that wasn't a delta above it. Otherwise it would display as a mu.
Subscripts simply wouldn't work at all. V_0 for example is supposed to display a V subscript 0, but it displayed nothing.
The code was gleaned from this site
Edit:
Apparently I can't attach more than one image, nor can I attach an image after I've removed it. I'll reply to this thread with the appropriate images.
Last edited: