Modeling the effects of GW and the "Earth Frame"

[GeorgeDishman]

First let me be clear, I am not questioning GR or the detection of gravitational waves by LIGO, I am trying to improve my own understanding of GW to the point where I can offer a graphic illustration (web video) showing what they do as they pass us to help others understand them. I started this a couple of years ago and thought I had a handle on it but have hit a problem with the LIGO parameters that tells me I have a misunderstanding somewhere. I don't know how to use GR mathematically (I have only a qualitative grasp) so I can't resolve the problem myself, and it probably comes from some remnant of Newtonian thinking that I've not recognised yet.

OK, the starting point was a pair of Wikipedia animations of the effects of GW:
https://en.wikipedia.org/wiki/File:GravitationalWave_PlusPolarization.gif
https://en.wikipedia.org/wiki/File:GravitationalWave_CrossPolarization.gif

The two particles at the left and right end can be thought of roughly as the two test mass mirrors in one LIGO arm while the top and bottom particles would be the mirrors in the second arm.

Those animations are just in a plane, to see how that is related to a wave, you need a 3D version like this:
http://www.einstein-online.info/images/spotlights/gw_wavesI/cyl_plus
Combining the polarisations might give this:
http://www.einstein-online.info/images/spotlights/gw_wavesI/gw_elliptic

Those are from this page
http://www.einstein-online.info/spotlights/gw_waves

The Wikipedia images can be thought of as a slice from the end of the einstein-online 3D tubes.

Those the effect of GW on a "ring of test particles" and I wanted to extend that to show the effect on a complete geodesic sphere enclosing a binary system system. The effect over any small region would be given by the equations in this part of the article (it's about the Earth-Sun system but the equations should be general):
https://en.wikipedia.org/wiki/Gravitational_wave#Wave_amplitudes_from_the_Earth.E2.80.93Sun_system

I intend to build up my understanding in steps so the simplest beginning was to consider a number of copies of the Wikipedia ring of particles with the horizontal ends sharing a particles (all are considered free-falling). It seemed to me that if one ring expanded, that next to it would have to expand too, alternating rings like this couldn't make sense:

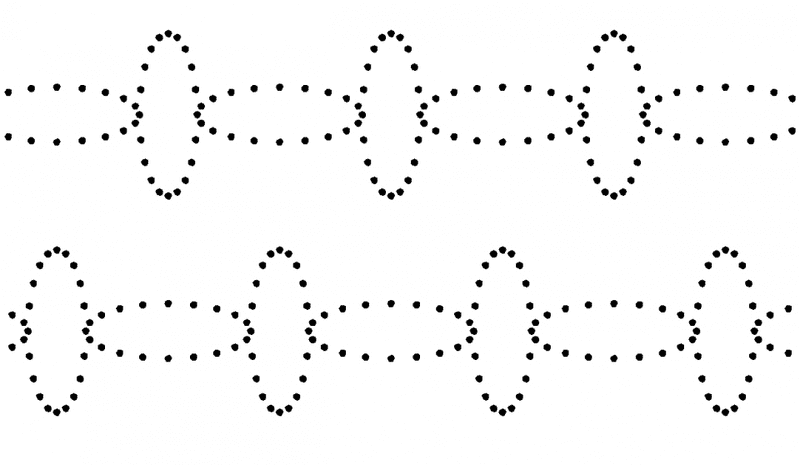
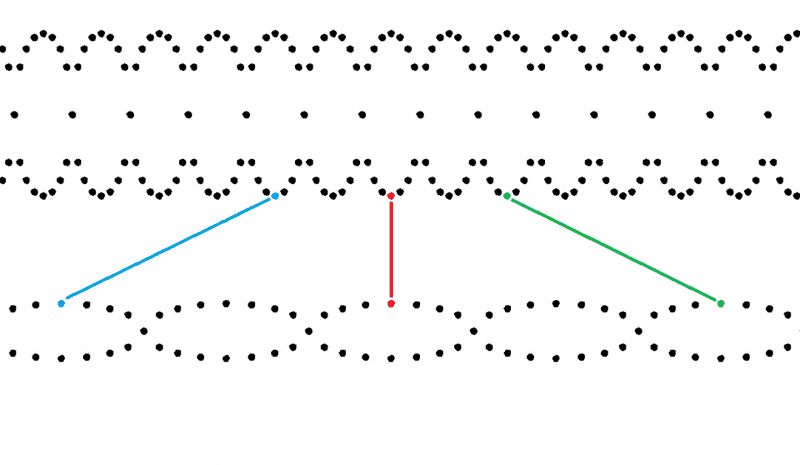
However, if all the rings are the same, then there is not only distortion but also displacement as shown by the coloured lines relating three of the particles. The red particle is used as a fiducial datum but see later:

That view seemed to be borne out when, some months later, I saw this explanation by Rainer Weiss in the LIGO press conference. The link should take you to 23:06 and you only need to watch 45 seconds or so:


Now if we extend Rainer's mesh into a ribbon that runs completely around the GW source at uniform radius, there is an obvious problem, how can the whole circumference expand or contract? The answer is that it doesn't. The frequency of the waves is double the orbital frequency of the binary system because, in the simplest case of equal masses, it doesn't matter which star is which. That means if we see expansion then at the same time an observer on the opposite side from us but at the same radius would also see expansion while observers half way round the circle would see contraction like this:

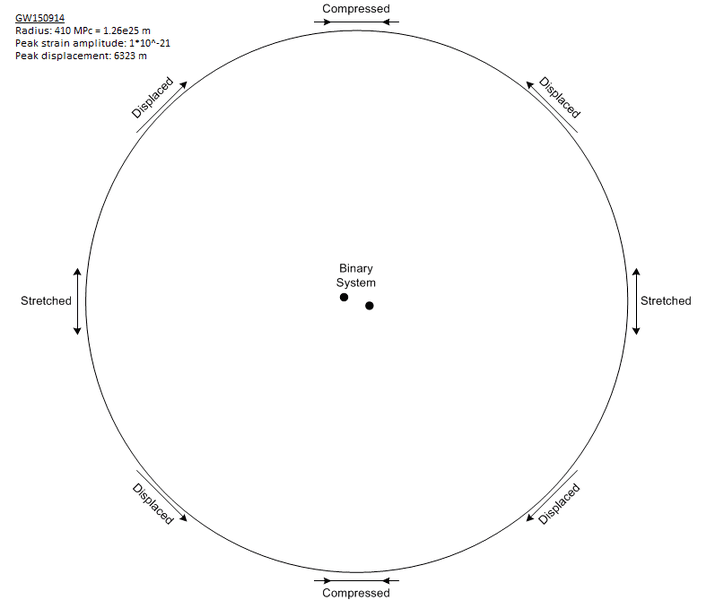
The numbers in the top left corner are for HM Cancri, the fastest nearby binary system. Now the expanded regions are balanced by contracted regions so the proper length round the circumference is constant.To find the displacement at any location relative to our fiducial point, we need to integrate the strain around the circumference. The strain is h sin(2θ) so the integral should be -h/2 cos(2θ) but that implies no part of the circumference is static.

Putting that together as a video (the start of my ultimate goal) gives me this image of Rainer's mesh extended all the way round (not to scale, think of it as light years round, 1m high and displacements of microns):

Again, it's only 30 seconds long so please watch it, the text will make a lot more sense if you do.

So why don't we measure the displacement? My view was that the two LIGO test masses can be thought of as lying at two adjacent points on the circumference and the beam tube is essentially the chord joining them. Since the beam tube and even the whole Earth are also displaced, there is no relative motion to be detected.

It should be clear that one point will be affected slightly before the other as the band of compression (say) moves round the circumference, hence what is measured can be thought of as the distance variation caused by the slight phase difference between the masses displacements.

In case anyone thinks I'm suggesting superluminal motion of the compression band round the circumference, I'll add this similar video showing how that is an illusion and what is really happening is a transverse wave propagating out from the binary system at the speed of light:


OK, I've typed enough, can anyone tell me where have I gone wrong or is this OK so far?

 

[PeterDonis]

can anyone tell me where have I gone wrong

You are missing a crucial point about the Wikipedia animations and the description of gravitational waves that they come from: that description is a linearized approximation, valid only in a small region of spacetime far from the source in which the small piece of the whole GW that is passing can be idealized as a perfectly transverse plane wave.

That means the following:

(1) You can't extend the "rings" indefinitely in any direction, because as you do, the direction in which the plane waves are propagating will change (think small pieces of an expanding spherical wavefront at slighly different angles from the source). That means the linearized approximation breaks down and the visualization you are using is no longer applicable.

(2) You can't visualize a big "ring" all the way around the source this way, because such a ring is obviously not a small region of spacetime far from the source in which a small piece of the whole GW can be idealiszed as a perfectly transverse plane wave. If you want to describe the global configuration of GWs on some sphere that completely encloses the source, you have to do it some other way; the linearized approximation is not valid and the visualization you are using is no longer applicable.

 

[GeorgeDishman]

You are missing a crucial point about the Wikipedia animations and the description of gravitational waves that they come from:

I suspect I'm missing more than one.

that description is a linearized approximation, valid only in a small region of spacetime far from the source in which the small piece of the whole GW that is passing can be idealized as a perfectly transverse plane wave.

That is true, the plane wave is an approximation to a variation of the distances on the surface of a sphere, but I understand the GR equations are differentials which need to be integrated, and if I take the limit as the ring size tends to zero then the chord length (which is the plane approximation) tends to the same as the arc length which would be the accurate version. Think of it as a piecewise linear approximation to a circle then taking the limit as the chord length goes to zero.

That means the following:

(1) You can't extend the "rings" indefinitely in any direction, because as you do, the direction in which the plane waves are propagating will change (think small pieces of an expanding spherical wavefront at slighly different angles from the source). That means the linearized approximation breaks down and the visualization you are using is no longer applicable.

The direction of propagation is perpendicular to the plane of each circle so each distance should still be valid as an approximation which becomes perfect when we take infinitesimals. However I can see that there would be a radial discrepancy using the plane wave approximation, but I think that is the nature of the approximation itself.

(2) You can't visualize a big "ring" all the way around the source this way, because such a ring is obviously not a small region of spacetime far from the source in which a small piece of the whole GW can be idealized as a perfectly transverse plane wave. If you want to describe the global configuration of GWs on some sphere that completely encloses the source, you have to do it some other way; the linearized approximation is not valid and the visualization you are using is no longer applicable.

OK so that's where I need the help from those members of the forum who understand GR. I've integrated the widely published equations at constant radius round the orbital plane and what that gives me seems logical but the numbers don't work out in the context of an "Earth frame" so what are the equations should I use instead? As I've said, I'm not someone who thinks GR is wrong, my aim is to produce a set of graphics like the ones you've seem that shows how a complete geodesic sphere of test masses would be displaced by the GW from a binary system. Finding out how to generate the graphics is the immediate task so if I can get the equations from a textbook or web reference in polar coordinates, that will let me move on. Just point me in the right direction please.

 

[PeterDonis]

the plane wave is an approximation to a variation of the distances on the surface of a sphere

Not just that. It is a linearized approximation to the nonlinear Einstein Field Equation. And the linearized approximation breaks down when you try to use it to cover too large an area of spacetime or a region in which spacetime curvature is too large.

I understand the GR equations are differentials which need to be integrated

I'm not sure what you mean by this. If you are referring to the "line element", the usual expression for the metric, yes that is written in the form of differentials because it describes a differential line element--the spacetime "length" of an infinitesimal curve between two events that are very close together. To get a "length" over a curve between two events at finite separation, you integrate the line element along the curve. But that only covers a very small part of what GR is used for.

If you are referring to the fact that the Einstein Field Equation is a differential equation, yes, that is true. But the primary thing that is done with the EFE in GR is to solve it, not to "integrate" it.

Think of it as a piecewise linear approximation to a circle then taking the limit as the chord length goes to zero.

I already understand how to get a linear approximation to a circle's chord. I'm pointing out that this method only applies in a limited set of scenarios, and the scenarios you are trying to consider (such as a "ring" going all the way around a source of GWs) are outside that limited set.

The direction of propagation is perpendicular to the plane of each circle so each distance should still be valid as an approximation which becomes perfect when we take infinitesimals.

As a bunch of individual approximations, each only applying to one particular small piece of spacetime, yes. But you are trying to put them all together into a single picture that covers more than a small piece of spacetime, but still assuming that all the laws of the linearized approximation will hold. That doesn't work.

I can see that there would be a radial discrepancy using the plane wave approximation

There would, yes, but that is not the only discrepancy. See above.

what are the equations should I use instead?

I don't know, because I don't know of any global solution describing a complete spacetime containing a source emitting GWs and the GWs themselves, over a large region, that can be expressed as closed-form equations. The only solutions of this kind that I'm aware of are numerical ones. You might look into the papers on binary pulsars to see if they give any descriptions of the kinds of numerical methods they're using; those are probably the most developed numerical GW solutions in existence.

 

[pervect]

Those the effect of GW on a "ring of test particles" and I wanted to extend that to show the effect on a complete geodesic sphere enclosing a binary system system.

I think this is where your problems start. If I'm understanding correctly (and I may not be), you are assuming that the gravitational waves are emitted in a spherically symmetric fashion from the central source.

But the problem lacks spherical symmetry. The problem has a cylindrical symmetry. The inspiral occurs in some spatial plane, the orbital plane of two large masses m1 and m2 which are orbiting each other. If we draw a sphere around this, the plane of the inspiral will define an "equator". The response of the gravitational wave detectors on the equator will differ from the response of the detectors on the poles.
.

The effect over any small region would be given by the equations in this part of the article (it's about the Earth-Sun system but the equations should be general):
https://en.wikipedia.org/wiki/Gravitational_wave#Wave_amplitudes_from_the_Earth.E2.80.93Sun_system

You can see this lack of spherical symmetry in the Wiki equations in the above article for $h_+$ and $h_x$, which represent the amplitude of the two components of the gravitational waves (GW's). The total amplitude of the GW would be $\sqrt{h^2_+ \,+\, h^2_x}$. Setting $\theta = 90^{\circ}$ corresponds to what I'm calling the equator, $0^{\circ}$ and $180^{\circ}$ correspond to what I'm calling the poles. If you inspect the above equations, you'll see that the amplitude of the components (and the total amplitude of the GW's) depends on the lattitude.

I intend to build up my understanding in steps so the simplest beginning was to consider a number of copies of the Wikipedia ring of particles with the horizontal ends sharing a particles (all are considered free-falling). It seemed to me that if one ring expanded, that next to it would have to expand too, alternating rings like this couldn't make sense:
View attachment 102997

Not a good idea - trying to have multiple centers in this manner is going to lead to confusion.

However, if all the rings are the same, then there is not only distortion but also displacement as shown by the coloured lines relating three of the particles. The red particle is used as a fiducial datum but see later:
View attachment 102998

There is displacement, yes. I would go so far as to say that that's what Ligo is measuring - it compares the displacements between the two arms.

That view seemed to be borne out when, some months later, I saw this explanation by Rainer Weiss in the LIGO press conference. The link should take you to 23:06 and you only need to watch 45 seconds or so:

...

Now if we extend Rainer's mesh into a ribbon that runs completely around the GW source at uniform radius, there is an obvious problem, how can the whole circumference expand or contract?

How I would describe what I think you're doing is that you're trying to describe the motion of the test particles relative to a rigid frame of reference.

The good news is that (assuming that you're doing what I think you're doing) there is an exact mathematical description of this viewpoint, it would be called a Born-rigid congruence. This viewpoint inherently has a "center" though. Roughly speaking, in this viewpoint we have one central object, and we define the motion of all nearby objects by saying that they are "at rest" relative to the central object, i.e. that their distance to the central object doesn't change. Under some conditions (including no rotation, though I won't get into the details), the objects at rest relative to the central object are also at rest relative to each other, and we have a rigid frame. Usually there are some fundamental constraints on the size of such a rigid frame, we don't expect it to cover all of space-time, just some local area that's "large enough" for some particular purpose we have in mind.

I believe you're trying to get rid of this center of your rigid frame. A possible motivation for what you're trying to do might be this. We've established that the GW's and the metric do depend on "lattitude", but does not depend on the longitude. So we might want a viewpoint that also doesn't depend on longitude. But the problem is - the "rigid frame" viewpoint, though highly intiutive, doesn't give us a viewpoint with these properties. The rigid frame viewpoint has a center.

So basically you're attempting to take a perfectly valid local viewpoint, that works great in a local area, and which has a center, and leverage it into a global viewpoint that doesn't have a center. The problem is that the local viewpoint just doesn't leverage in this manner.

The existence of a center is a property of the viewpoint and one that can't be gotten rid of by drawing "multiple circles", and attempting to create multiple centers. The whole structure collapses when you try to do this :(. To follow the "rigid frame" idea, you need to stick with one center, that defines your viewpoint, and realize that the viewpoint itself has limits. To expand those limits requires a different starting viewpoint.

The good news is that while the viewpoint has limits, it should be perfectly adequate to encompass the entire Earth.

I won't talk about alternatives to rigid frames - it's already confusing enough I think. But if I'm totally off track on what you're trying to do, I suppose that we'd have to discuss just what it is that you're trying to do to get anywhere.

 

[GeorgeDishman]

I think this is where your problems start. If I'm understanding correctly (and I may not be), you are assuming that the gravitational waves are emitted in a spherically symmetric fashion from the central source.

No, I am assuming that the simplest form is axisymmetric and that would apply only for a specific configuration of the spins of the binary components. It might be that they are not rotating or perhaps tidally locked or possibly any rotation as long as the angular momentum vectors of the components are in the same direction as that of the orbit.

In general, I appreciate that there is no symmetry at all. For example, thinking about the merger phase, for a binary orbiting in the x-y plane, GW can be preferentially emitted in the -z direction giving the resultant product a kick in the +z direction, and the earlier inspiral must show the same effect though to a much lesser extent.

What I am modelling is not a fully general solution but only the simplest subset.

But the problem lacks spherical symmetry. The problem has a cylindrical symmetry. The inspiral occurs in some spatial plane, the orbital plane of two large masses m1 and m2 which are orbiting each other. If we draw a sphere around this, the plane of the inspiral will define an "equator". The response of the gravitational wave detectors on the equator will differ from the response of the detectors on the poles. ... If you inspect the above equations, you'll see that the amplitude of the components (and the total amplitude of the GW's) depends on the lattitude.

Exactly. I'm starting on the equator but the aim is to extend that to show how the two polarisations combine to alter the distortion as the 'latitude' varies.

There is displacement, yes. I would go so far as to say that that's what Ligo is measuring - it compares the displacements between the two arms.

Yes, that is what I felt was confirmed by Rainer Weiss's presentation, although obviously that is very much aimed at the public.

How I would describe what I think you're doing is that you're trying to describe the motion of the test particles relative to a rigid frame of reference.

The good news is that (assuming that you're doing what I think you're doing) there is an exact mathematical description of this viewpoint, it would be called a Born-rigid congruence. This viewpoint inherently has a "center" though. ... Under some conditions (including no rotation, though I won't get into the details), the objects at rest relative to the central object are also at rest relative to each other, and we have a rigid frame. Usually there are some fundamental constraints on the size of such a rigid frame, we don't expect it to cover all of space-time, just some local area that's "large enough" for some particular purpose we have in mind.

That's precisely what I'm trying to do, at least for the animations.

I believe you're trying to get rid of this center of your rigid frame.

Not at all, sorry if I gave that impression. The viewpoint for the movies is a Born rigid sphere whose centre is the barycentre of the binary system. The example I started with about a year ago was HM Cancri which is 1600 light years away (but I'm ignoring the other stars in the galaxy of course) so it would be a non-rotating sphere of 1600 light years radius.

We've established that the GW's and the metric do depend on "lattitude", but does not depend on the longitude.

Yes, and eventually I hope to model that variation with latitude, but I hit a problem just on the equatorial picture when I started thinking about how the "Earth frame" that was mentioned in the previous thread would relate to the picture relative to the Born rigid picture so I'm trying to resolve that before proceeding.

I won't talk about alternatives to rigid frames - it's already confusing enough I think. But if I'm totally off track on what you're trying to do, I suppose that we'd have to discuss just what it is that you're trying to do to get anywhere.

You've got 99%, it just needed the clarification that the centre of the Born-rigid sphere is the barycentre of the binary system, and I appreciate the solution is axisymmetric. It is perhaps also worth noting that I'm only using the rigid sphere as a viewpoint, essentially a set of fiducial points that have no input to the physics. Applying this to the real world will then note that the Earth is also an object that is free to be displaced and to distort in response to the GW, that's where my problems arise.

I think my concern at this stage would be to take Peter's point and question whether it is valid to sum (integrate) a large number of width changes to get the total displacement relative to the rigid reference sphere. I'm just starting to learn MATLAB to do the modelling so I have used a simple square mesh in my video, but each cell of that can be likened to Wikipedia ring of test particles, and for size perhaps think of two adjacent nodes on the mesh being the test masses in LIGO.

My understanding was that the Wikipedia images show a ring of particles in a plane relative to a fiducial point in the centre. My series of rings treats each ring as being in a slightly different flat plane, only the end particles of adjacent rings are common to both rings. Integrating the end particles separations round the equator suggests to me that we can think of each whole ring as also translating round the 'equator', but of course that isn't detectable locally. For example an infinitely sensitive accelerometer in space would always show zero even though it was being displaced 'east' and 'west' in a sine wave the particles are all following geodesics (other than ignoring the low decrease of radius).

P.s. I should say I am also considering the situation of a steadily orbiting system. HM Cancri for example is several hundred thousand years from merging (IIRC) and has an orbital period of 321.5 seconds so I am ignoring evolution of the orbit and GW.

 

[PeterDonis]

The viewpoint for the movies is a Born rigid sphere whose centre is the barycentre of the binary system.

I don't think that's what pervect meant when he brought up Born rigidity (he will correct me if I'm wrong, of course). I think he was talking about a Born rigid congruence describing a local reference frame in which the linearized approximation holds.That certainly isn't true for a large, 1600 light year sphere centered on some binary system. (Even for the localized case there are issues with trying to make use of Born rigidity, since the test masses in a localized GW detector do not form a Born rigid congruence--if they did they could not detect GWs.)

Moreover, the binary system itself is not Born rigid and can't be described by a Born rigid congruence.

 

[pervect]

I don't think that's what pervect meant when he brought up Born rigidity (he will correct me if I'm wrong, of course). I think he was talking about a Born rigid congruence describing a local reference frame in which the linearized approximation holds.That certainly isn't true for a large, 1600 light year sphere centered on some binary system. (Even for the localized case there are issues with trying to make use of Born rigidity, since the test masses in a localized GW detector do not form a Born rigid congruence--if they did they could not detect GWs.)

Moreover, the binary system itself is not Born rigid and can't be described by a Born rigid congruence.

I basically agree with Peter's comments.

We can find an approximately Born-rigid congruences in a sphere around, say, the Earth, which is a large distant away from the gravitational wave source, where we make the approximations (linearizations) that Peter is talking about. Whether or not we can find such a scheme that works around the strongly-gravitating source is problematical.

I've had some discussions (and perhaps even arguments) here on PF recently over similar points, and found what looks like a good reference on this point. http://arxiv.org/pdf/gr-qc/0511041.pdf. But it may be rather advanced.

The simplest choice for a physically significant spatial metric is:
$$\bar{g}_{ab} = \hat{g} \quad where \quad \hat{g}_{\alpha\beta} := g_{\alpha\beta} + u_{a} u_{b}$$
i.e. the quotient or Fermat metric. But, it is a well-known fact that this metric is rigid only for a very short class of congruences.

[Cartan] Any Riemannian manifold that admits movements that do not deform the geometry of a figure (satisfies the free mobility axiom), is maximally symmetric, that is, has constant curvature.

The GW source, does not have constant curvature.

Based on this paper, I now believe that we cannot (as others have suggested) find a perfectly Born-rigid congruence for a GW with the usual (Fermat) definition of the spatial metric (i.e. the usual definition of distance). The theorem mentioned by Cartan would seem to prevent it. The authors of the above paper suggest one way around this difficulty by modifying our notion of distance so that we can find an exactly "rigid" metric and congruence (using their new defintion which is very similar to the old one.)

But more importantly, however, by taking advantage of the fact that the we describe GW's by a linearization process as a pertubation of some flat spatial metric $\eta_{\mu\nu}$, we can find an "approximately rigid" congruence by ignoring the perturbative part of the gravity wave to create an approximately rigid frame. In another thread I've done some calculations for the "almost rigid" congruence. No expansion would represent ideal rigidity (we can ignore shear for now, as it turned out to be zero). The expansion measured by Ligo for the freely-floating test masses (which are not rigid, we are measuring the distance changes!) is on the order of $10^-21$ or so - barely detectable with our best equipment. The expansion of the "almost rigid" congruence would be second order, i.e. 10^-42 or so. So our approximation is more than good enough to draw a diagram, even if a mathematician might tell you, quite honestly, that there was no mathematical solution that was perfectly rigid.

Going from this approximate notion far from the source to saying that we can do the same in the strong-field region around the GW source is a bit of a stretch. I'm rather skeptical, I'd need to see the numbers. I rather doubt anyone has tried, though. One might get an idea of how accurate such a scheme would be by looking at the metric close-in (where you want to draw your diagram) and looking at how large the pertubations from flatness are. The one thing that might save you is that the approximations are so good distant from the source that they still might be "good enough" up closer. However, I don't have the data to do so, and I'm not sure if it's available or not.

So basically my suggestion is to consider a different problem - not around the source, but around the receiver. I'm pretty sure that's the intended use of the various illustrations you cite - not a sphere around the source, but rather a sphere around the receiver.

You can view the source as a curved 4-dimensional geometry using the "block universe" approach. But visualizing this directly doesn't seem promising.
...

 

[pervect]

Some more technical details of a new calculation: the last analysis I did was only 1 space + 1 time, at this point I felt that it would be productive to check the full 3space 1time case. I used the following metric for a linearized plus polarized plane GW:

$$g = -dt^2 + (1+2 \,k \,f(t-z))dx^2 + (1-2\,k\,f(t-z))dy^2 + dz^2$$

This is a plane wave metric far from the emission source - it's approximate because the metric itself is only accurate to linear order (terms of order k), and it's approximate because we've assumed the GW is a plane wave, whereas the actual wavefronts would have a spherical symmetry.

k represents the strength of the wave, a small dimesionless constant of approximately 10^-21 or so for Ligo. f and it's derivatives are considered to be not large, are x,y, and z.

Then I looked at the expansion and shear for the geodesic congruence (i.e. a congruence of freely floating test masses). For the given metric/line element, geodesic curves are just curves where x,y, and z have constant coordinate values. Formally, we can write the congruence as $\partial_t$. This calculation is for informational purposes - we know the test masses are moving relative to each other, that's what Ligo is measuring. We calculate it to have some idea of the significance of the numbers we calculate. The expansion has terms of order k^2, the shear has terms of order k. So the presence of a shear term of order k means that the GW's stretch our congruence by a factor of k, as in the illustrational videoes with the mesh being pulled apart, and the GW's change the area by a smaller amount, a factor of k^2.

Next I looked at the "approximately rigid" congruence. This attempts to compensate for the motion of the test masses in what in retrospect is an obvious manner - basically one assumes that the changing separation in the x direction is due to some velocity v in the x direction, a velocity which is proportional to the distance from some refererence point which is taken as "not moving". One adds a similar velocity in the y direction. Formally we can write this congruence as:

$$\partial_t -k\,\frac{\partial f(t-z)}{\partial t} \,x\,\partial_x + \frac{\partial f(t-z)}{\partial t} \, y \, \partial_y$$

After normalizing the above vector to unit magnitude, we find (with the aid of a computer to do the scut work) that the expansion of the almost-rigid congruence is of order k^3 and the shear is of order k^2. So both expansion and shear were multiplied by a factor of k, making them "small". Informally, my argumemnt for why this works is that the GW metric is "almost Minkowskian", and the "almost Minkowskian" property gives rise to an "almost rigid" congruence.

[add]There's some issues. It appears there are some linear-order terms in the xz and yz components of the shear tensor. So it's not quite accurate to second order :(

 

[GeorgeDishman]

Some more technical details of a new calculation: the last analysis I did was only 1 space + 1 time, at this point I felt that it would be productive to check the full 3space 1time case. I used the following metric for a linearized plus polarized plane GW:

$$g = -dt^2 + (1+2 \,k \,f(t-z))dx^2 + (1-2\,k\,f(t-z))dy^2 + dz^2$$

This is a plane wave metric far from the emission source - it's approximate because the metric itself is only accurate to linear order (terms of order k), and it's approximate because we've assumed the GW is a plane wave, whereas the actual wavefronts would have a spherical symmetry.

This is just a quick note, I've downloaded the paper you cited and I need to mull over your other post too, but I think what I am trying to do might be similar to turning the above into polar coordinates and then solving in 2 space + time for constant radius (i.e. z -> R = constant).

This next bit is honestly beyond my level but I think roughly, for a binary a long time from merger (compared to the orbital period), what I am doing is treating the waves far from the binary as a perturbation on the Schwarzschild metric where the mass is something like the ADM mass but excluding the energy outside radius R. I think this is similar to the "chirp mass" of the system.

Also, I think you're on the right track when you say "Based on this paper, I now believe that we cannot (as others have suggested) find a perfectly Born-rigid congruence for a GW with the usual (Fermat) definition of the spatial metric (i.e. the usual definition of distance).". That is probably the key to my problem

So basically my suggestion is to consider a different problem - not around the source, but around the receiver.

I may also be able to reformulate the question into a small volume containing the Earth but unfortunately it will still have to relate back to the bigger picture.

I'm pretty sure that's the intended use of the various illustrations you cite - not a sphere around the source, but rather a sphere around the receiver.

All the external sources I've cited are for a small region far from the source and illustrate the local strain for the linear, plane wave solution. The two Vimeo animations are my own and represent the picture with the binary in the centre. If you look at just one cell in the cylindrical mesh, that relates to all the other commonly available animations.

 

[GeorgeDishman]

k represents the strength of the wave, a small dimesionless constant of approximately 10^-21 or so for Ligo. f and it's derivatives are c

Is your 'k' the same as LIGO's 'h' term?

The expansion has terms of order k^2, the shear has terms of order k. So the presence of a shear term of order k means that the GW's stretch our congruence by a factor of k, as in the illustrational videoes with the mesh being pulled apart,

That puzzles me a bit, I would have thought "stretch" related to "expansion" rather than shear so I guess I'm unfamiliar with the terms here. Could you add a little guidance on that please.

and the GW's change the area by a smaller amount, a factor of k^2.

That definitely confuses me, I thought any volume would be 'stretched' in say x but squished in y so that the area remained constant. That seems to fit the animations and it made sense if there is no z variation because the waves are akin to a tidal effect and I thought tidal variations preserved volume. If our small test ring of particles having radius r is distorted by a strain of k, it should be an ellipse with semi-major axis a=kr and semi-minor axis b=r/k. The area is πab so remains πr².

The more I learn, the less it seems I know (which I take as a good thing BTW, exposing one's lack of knowledge is the first step to learning).

 

[GeorgeDishman]

I used the following metric for a linearized plus polarized plane GW:

$$g = -dt^2 + (1+2 \,k \,f(t-z))dx^2 + (1-2\,k\,f(t-z))dy^2 + dz^2$$

This is a plane wave metric far from the emission source - it's approximate because the metric itself is only accurate to linear order (terms of order k), and it's approximate because we've assumed the GW is a plane wave, whereas the actual wavefronts would have a spherical symmetry.

This is extreme guesswork as is no doubt obvious, but:

• the waves can have different rates, should f(t-z) be f(ωt-2π(z/λ)) where ω is the angular frequency and λ is the wavelength?
• can that metric be adjusted to take account of the phase around the equator of the circle with the source at the centre by using f(ωt-2φ-2π(z/λ)) where φ is the azimuth in spherical coordinates (hence dx=R dφ and dy=R dθ with z≡R) ?

P.S.

Going from this approximate notion far from the source to saying that we can do the same in the strong-field region around the GW source is a bit of a stretch. I'm rather skeptical,

I agree and I'm not trying to do that, I only want to model a spherical shell with a thickness of just a few AU and at a uniform radius no less than a thousand light years from the source. Any sort of strong field or "near field" effects (analogous to EM) are well beyond my scope.

 

[PeterDonis]

I think what I am trying to do might be similar to turning the above into polar coordinates and then solving in 2 space + time for constant radius (i.e. z -> R = constant).

If what you mean by polar coordinates is polar coordinates centered on the source, this will not work. The metric pervect gave is only valid in a small piece of spacetime far from the source in which the GW can be idealized as a purely transverse plane wave. That will obviously not be true in polar coordinates centered on the source.

 

[GeorgeDishman]

I don't think that's what pervect meant when he brought up Born rigidity (he will correct me if I'm wrong, of course). I think he was talking about a Born rigid congruence describing a local reference frame in which the linearized approximation holds.That certainly isn't true for a large, 1600 light year sphere centered on some binary system. (Even for the localized case there are issues with trying to make use of Born rigidity, since the test masses in a localized GW detector do not form a Born rigid congruence--if they did they could not detect GWs.)

I agree completely, I have only been talking about a Born rigid congruence in the sense of a set of fiducial points for reference formed as a sphere around the binary at uniform radius but nowhere have I suggested that the plane wave equations would be able to describe the bigger picture.

Moreover, the binary system itself is not Born rigid and can't be described by a Born rigid congruence.

Of course not, nothing physical in this scenario is Born rigid.

I basically agree with Peter's comments.

So do I.

The only purpose of introducing the concept of the Born rigid congruence is to provide a notional reference against which true geodesics can be measured. Ultimately, the only measurables are between physical objects (test masses, the Earth or eLISA satellites), each of which can hopefully be described via deviation from this common reference congruence. If we know how A and B each move relative to R, it should be possible to find out how A moves relative to B.

If what you mean by polar coordinates is polar coordinates centered on the source, this will not work. The metric pervect gave is only valid in a small piece of spacetime far from the source in which the GW can be idealized as a purely transverse plane wave. That will obviously not be true in polar coordinates centered on the source.

Sorry, I should have said spherical coordinates.

You are quite right again, but I have nowhere suggested using that metric which is defined for plane waves over a sphere. What I think is needed is a different metric defined in spherical coordinates but which is locally asymptotic to the one pervect quoted. I've already suggested a possible modification but I doubt it is correct, I am just hoping it is something that can prompt some constructive suggestions as to how to resolve the problem.

 

[PeterDonis]

The only purpose of introducing the concept of the Born rigid congruence is to provide a notional reference against which true geodesics can be measured.

But this "notional reference" doesn't exist, so you can't measure anything against it.

 

[GeorgeDishman]

But this "notional reference" doesn't exist, so you can't measure anything against it.

Caught me, yes that was a bit of bad typing. I said it correctly a few lines later:

If we know how A and B each move relative to R, it should be possible to find out how A moves relative to B.

Nothing gets measured relative to R, A only gets measured relative to B, but R can be a useful intermediate in calculating the predicted motions. This goes back to the previous thread where we noted that a "fiducial point" does not have a physical significance:

It is true that, in principle, any choice of chart should give the same values for actual observables like the interference pattern at the photodetector, so in that sense the choice of fiducial point doesn't matter.

 

[PeterDonis]

Nothing gets measured relative to R, A only gets measured relative to B, but R can be a useful intermediate in calculating the predicted motions.

Ah, I see, you are interpreting "R" as a coordinate (or something that gets defined relative to a coordinate chart), not an actual object.

 

[pervect]

But this "notional reference" doesn't exist, so you can't measure anything against it.

If we look at some of the material and diagrams posted by the OP, for instance: https://en.wikipedia.org/wiki/File:GravitationalWave_PlusPolarization.gif we can ask the question: what motivates these diagrams as a 2-d cross section of a GW?

If our notional rigid reference frame doesn't exactly exist, what motivates them?

I've suggested variously that they could be motivated by looking at the appropriate tangent space, or they could be motivated by a frame that is rigid in the unperturbed flat space-time (but is only aproximately rigid in the actual GW space-time).

 

[PeterDonis]

what motivates these diagrams as a 2-d cross section of a GW?

The way the metric looks in the transverse-traceless (TT) coordinate chart, which is the one in which you wrote down the linearized metric. In that chart, each little dot in the diagrams has constant spatial coordinates (x, y, z), so the only source of variation in the physical distance between them is the variation in the correction terms in $g_{xx}$ and $g_{yy}$. The variation in physical distance is what the diagrams portray.

they could be motivated by a frame that is rigid in the unperturbed flat space-time (but is only aproximately rigid in the actual GW space-time).

This is more or less what the TT coordinate chart does--constant spatial coordinates in this chart basically amounts to "would be rigid if spacetime were unperturbed" (at least to linear order).

 

[pervect]

The way the metric looks in the transverse-traceless (TT) coordinate chart, which is the one in which you wrote down the linearized metric. In that chart, each little dot in the diagrams has constant spatial coordinates (x, y, z), so the only source of variation in the physical distance between them is the variation in the correction terms in $g_{xx}$ and $g_{yy}$. The variation in physical distance is what the diagrams portray.
This is more or less what the TT coordinate chart does--constant spatial coordinates in this chart basically amounts to "would be rigid if spacetime were unperturbed" (at least to linear order).

But in those coordinates, the test masses follow geodesics, which means that x, y, and z are all constant. So if we take a slice z=0, and we plot the coordinates x and y for a set of test masses in this coordinate system, we would represent the motion of the test masses by points on the diagram with constant coordinates - which makes for a boring diagram where the points don't move.

So the first thought that comes to my mind is that we are plotting the motion of the slice (z=0), but we are not plotting it in a coordinate basis, but in an orthonormal basis with unit vectors $\hat{x}$ and $\hat{y}$ given in terms of the TT coordinates as $\hat{x} = \sqrt{1+2kf(t-z)} \, \partial_x \approx (1+kf(t-z)) \, \partial_x$ and $\hat{y} = \sqrt{1-2kf(t-z)} \, \partial y \approx (1-kf(t-z)) \, \partial_y$. But this interpretation means we are plotting the points not on the manifold, but in the tangent space, where $\hat{x}$ and $\hat{y}$ are defined.

A second thought is that there should be some actual coordinate basis, different from the ones I wrote down, where the motion looks like the diagram, and that these coordinates should be physically interesting.

 

[PeterDonis]

in those coordinates, the test masses follow geodesics, which means that x, y, and z are all constant.

Yes, but that doesn't make the physical distance between them constant; it only makes the coordinate distance between them constant. The metric is changing with time--specifically, $g_{xx}$ and $g_{yy}$ are changing with time--and so the relationship between coordinate distance and physical distance, at least in the x-y plane, is changing with time. Basically, the unchanging coordinate distance represents "would be rigid if spacetime were unperturbed", and the changing physical distance, which is what the Wikipedia diagrams show, represents "how spacetime is perturbed" as seen in these coordinates.

 

[GeorgeDishman]

These comments go back to the previous thread where I asked whether the test masses actually move relative to the LIGO beam tube ends. I think I finally found a document that helps. Have a look at lectures 15 an 16 starting on page 103 (of 150) here, and in particular the conclusion of section 4 of lecture 16 on page 108:

edaw.staff.shef.ac.uk/most.pdf

"So a particle that was moving at a fixed velocity along the x-axis in the absence of gravitational wave has the velocity of its motion modulated with the period of the gravitational wave as the wave is passing through. On the other hand a particle that is not moving in the absence of the gravitational wave remains stationary as the wave passes. The manifestation of the wave is the modulation of the coordinate velocity of light in the plane normal to the direction of incidence of the wave as it passes through. ... The coordinate system where the masses stay at fixed coordinate positions and the speed of light oscillates is called 'transverse traceless'. ... If you fix two mirrors a distance L apart on the x axis, then allow a gravitational wave to pass through, how long does a light beam take to pass between the mirrors? Because the mirrors are initially stationary, they do not move in this coordinate system."

If that is correct, obviously my integration of the expansion to get displacement is pointless, it will be zero too of course, but that solves my problem!

However, does the separation of the ends of the LIGO beam tubes stay constant in transverse traceless coordinates?

More importantly, what is meant by the "Earth Frame" in this coordinate system

• (a) where the wavelength of the GW is much greater than the diameter of the Earth, λ>>D_E and
• (b) when λ<<D_E ?

 

[pervect]

These comments go back to the previous thread where I asked whether the test masses actually move relative to the LIGO beam tube ends. I think I finally found a document that helps. Have a look at lectures 15 an 16 starting on page 103 (of 150) here, and in particular the conclusion of section 4 of lecture 16 on page 108:

edaw.staff.shef.ac.uk/most.pdf

"So a particle that was moving at a fixed velocity along the x-axis in the absence of gravitational wave has the velocity of its motion modulated with the period of the gravitational wave as the wave is passing through. On the other hand a particle that is not moving in the absence of the gravitational wave remains stationary as the wave passes. The manifestation of the wave is the modulation of the coordinate velocity of light in the plane normal to the direction of incidence of the wave as it passes through. ... The coordinate system where the masses stay at fixed coordinate positions and the speed of light oscillates is called 'transverse traceless'. ... If you fix two mirrors a distance L apart on the x axis, then allow a gravitational wave to pass through, how long does a light beam take to pass between the mirrors? Because the mirrors are initially stationary, they do not move in this coordinate system."

If that is correct, obviously my integration of the expansion to get displacement is pointless, it will be zero too of course, but that solves my problem!

However, does the separation of the ends of the LIGO beam tubes stay constant in transverse traceless coordinates?

More importantly, what is meant by the "Earth Frame" in this coordinate system

• (a) where the wavelength of the GW is much greater than the diameter of the Earth, λ>>D_E and
• (b) when λ<<D_E ?

I would interpret these remarks in terms of the coordinate system I used in #9, which is a common means of describing plane GW's, so I believe from context and frome experience that that's the coordinate system the author is using. This coordinate system is simply not a rigid frame. I believe you're interpreting the author's remarks which were made in this non-rigid-frame context as if they were made in a rigid frame point of view.

The motion in the coordinate system of #9 is pretty simple. Anything at rest stays at rest, unless subject to an external force. Where "by at rest", one means "with constant coordinates". Alternatively, one might say that particles in natural (i.e. geodesic) motion have constant coordinates. This matches up with what your source is saying.

In these coordinates, the particles are "at rest", but the distance between them still increases. It has to, of course, that's what Ligo is measuring. But while the particles are "stationary", the distance between them is still changing. This is explained via the metric. The coordinates stay constant, but the distance that the coordinates represent does not stay constant, the distance increases. This leads to the "expanding space" point of view, similar to the "expanding space" point of view used in cosmology. Objects at rest with respect to the Hubble flow in cosmology are considered to be "at rest", but the distance between them still increases.

The expanding space point of view is a perfectly fine viewpoint (though I would personally avoid talking about changing the speed of light, this tends to cause totally unnecessary confusion and digression). The problem arises is when remarks made in the expanding space point of view, which is definitely a non-rigid frame, frame, are taken as if they were made about the rigid frame. Similar confusions arise with the same concept in cosmology, but it would be a distraction to pursue the analogy over much here, though I will leave in a brief mention of it.

So let's look at the part of the author's remarks that is the issue, the highlighted part:

a particle that is not moving in the absence of the gravitational wave remains stationary as the wave passes.

This is true if the particle is a free particle, not attached to anything. But this is true of the test masses, it's not true for the beam tube. Since the distance between the ends of the beam tube is not changing appreciably (because the beam tube is stiff), and the distance between the test masses is changing, one can conclude that the test masses are moving differently from the particles in the beam tube, that they are moving relative to the beam tube. The author you quote doesn't say otherwise - he simply isn't interested in explaining the motion of the beam tube.

What's happening is that the passing GW is causing stresses in the beam tube, as the particles in the beam tube try to keep their distance constant, and (mostly) succeed. So the particles in the beam tube are not force-free particles, and the particles in the beam tube do move relative to the free-floating particles following geodesics. Everyone will agree that there is relative motion, but confusion arises with this point of view due to the tendency of people to assume that the beam tube is not moving, when the coordinate system used in the "expanding space" point of view assumes instead that the suspended test masses as "not moving".

[add]
My general approach is to try to explain things from the point of the beam-tube, rather than the point of view of the test masses. This point of view can't be "exactly" rigid, but we can hopefully make it approximately rigid. I thought I had it down, but it appears that under closer inspection there are some glitches in the z direction. So,while I think there should be such an explanation, I'd have to say at the current time I don't have one.

So I suppose the bottom line is that what happens to the test masses in the Ligo experiment is well defined and calculated, and the results are expressed as a metric. The issue is that the usual calculation isn't in a "rigid frame", nor anything that even in an approximate sense resembles a rigid frame, so the results of the calculations may need to be communicated without this concept at the current time, which is proving difficult.

What happens to the Earth is not calculated or even discussed anywhere that I've run into so far and appears to be trickier than I would have thought when I look at it myself - except perhaps to say it's very small, but we can't yet quantify it to say that it's smaller than the motions of the test masses.

 

[pervect]

One optimisitic thing I should add. I've got a perfectly adequate description of what happens if a GW impacts a flat plate in terms of a quasi-rigid plate. And this description matches the two dimensional diagrams from the wiki article. In this description, the test masses move relative to the plate, with a velocity that's proportional to the distance from the center of the plate. And the distance between points on the plate is rigid to the second order in k. This description just doesn't seem to be generalizaing well to a quasi-rigid cube, at least not at the moment.

 

[PeterDonis]

a particle that is not moving in the absence of the gravitational wave remains stationary as the wave passes.

This sense of "remains stationary" is a bit misleading. What he means is that the spatial coordinates of the particle do not change. But the physical spatial distance between two particles at constant spatial coordinates does change (at least if the distance is in the x-y plane), because of the change in the metric coefficients. (See my response to pervect in post #21.)

The lecture calls this a "change in the coordinate speed of light", but one has to be careful interpreting this statement. His justification for the coordinate speed of light changing is that he calculates $dx / dt$ for a light ray in his coordinates and finds that it is not a constant $c$; it is $c$ plus a small oscillating term. However, that does not mean that spatial distances cannot also change. To see whether spatial distances change, you have to look at the distance between two particles at constant spatial coordinates $(x_1, y_1)$, $(x_2, y_2)$ in a spacelike surface of constant coordinate time. If you calculate this, you will find that it also works out to a constant (which is just the Pythagorean theorem distance between those two spatial coordinates in flat space--the lecture would probably call this the "coordinate distance", and it is what is being referred to when it is stated that the masses are "fixed") plus a small oscillating term. So spatial distances change with time in these coordinates by the same argument that shows that the coordinate speed of light changes with time.

I don't think these two things--changing coordinate speed of light and changing physical spatial distances--are "different effects" in the sense of being two different physical things that are both going on. I think they are just different manifestations of the same physics. But I think it's important not to lose sight of the fact that both of these manifestations are present. The second manifestation, that spatial distances change, is what pervect is referring to when he says the reference frame is not rigid: the motion of the test masses is not a Born rigid motion. (To be Born rigid, the physical spatial distances would have to be unchanging, not the coordinate distances.)

 

[GeorgeDishman]

Thanks for both your comments, they echo precisely what I was thinking based on your previous remarks and the paper. I think the penny has finally dropped.

Similar confusions arise with the same concept in cosmology, but it would be a distraction to pursue the analogy over much here, though I will leave in a brief mention of it.

My background is that I am an admin in a cosmology group and I've completed the Coursera offering on cosmology by Prof. Djorgovski of Caltech so that analogy is perfect for me.

The expanding space point of view is a perfectly fine viewpoint (though I would personally avoid talking about changing the speed of light, this tends to cause totally unnecessary confusion and digression).

That's actually something I now need to verify. Suppose the speed of light is isotropic and has the value c₀ in the absence of a wave. If a plane wave propagating in the z direction passes, for the cross polarisation in the x-y direction, it appears that in these coordinates the speed would become anisotropic with c_z=c₀, c_x=c₀(1+h*sin(φ)) and c_y=c₀(1-h*sin(φ)) where φ is the phase of the wave and h is the amplitude (though you mention "there are some glitches in the z direction"). Am I right in thinking that would be a tensor? As I say, my maths in this area is rudimentary to say the least!

In these coordinates, the particles are "at rest", but the distance between them still increases. It has to, of course, that's what Ligo is measuring. But while the particles are "stationary", the distance between them is still changing.

Yes, if the metre is defined as the distance traveled in 1/299792458 seconds then a change in the speed of light alters the distance without the particles being moved.

On the other hand, the beam tubes are affected by the change of speed so they would effectively shrink and stretch as the wave passed in these coordinates. It's a peculiar viewpoint but it works for me.

 

[GeorgeDishman]

This description just doesn't seem to be generalizaing well to a quasi-rigid cube, at least not at the moment.

That is where I think the "Earth frame" comes in. I think we would model this as a plane wave passing over a quasi-rigid sphere of (nearly) uniform density, bulk and shear modulus. For λ>>D_E, that is probably identical to your plate version (but a disc of course). For λ<<D_E, slicing the Earth would make it look like a sheaf of such discs but although they would relatively unmoving at the centre on an axis in the z direction, they would have differing relative velocities, increasing in proportion to the radius. You therefore have to consider the shear effect in a solid sphere and my impression is that it would look like conventional "solid tides" as created by the Moon.

http://www.navipedia.net/index.php/Solid_Tides

Once that is resolved, you can consider the effect on the surface which is where LIGO is located which will also depend on the orientation of the wave to the arms, that is exactly why I included the mention of the "Earth Frame" in the title, it's not a trivial question.

 

[GeorgeDishman]

... my impression is that it would look like conventional "solid tides" as created by the Moon.

Just to clarify, I didn't mean the solution would be the same, just that the same physics is involved in creating the effects.

Once that is resolved, you can consider the effect on the surface which is where LIGO is located which will also depend on the orientation of the wave to the arms, that is exactly why I included the mention of the "Earth Frame" in the title, it's not a trivial question.

This goes back to the earlier thread, the apparent motion of the masses relative to the tube ends is probably most easily calculated by finding the motion of the tube ends in the frame where the masses are motionless.

 

[GeorgeDishman]

I've just realized there was a typo in my earlier reply that hid what I was saying:

If our small test ring of particles having radius r is distorted by a strain of k, it should be an ellipse with semi-major axis a=kr and semi-minor axis b=r/k. The area is πab so remains πr².

The strain amplitude k is the maximum change from the rest length so that should have read:
".. semi-major axis a=(1+k)r and semi-minor axis b=r/(1+k). The area is πab so remains πr²."

What I'm saying comes from the view of the effect as a multiplicative scaling (similar to the "scale factor" in cosmology) so when contracted, sizes decrease to r/(1+k). When we look at the deviation from a rest position however, we generally make use of the approximation r/(1+k)≈r(1-k) hence the peak displacement becomes ≈±kr.

When we use that to calculate the area however, we get A=πab≈πr²(1+k)(1-k)≈(1-k²) so I think the apparent second order variation in area is actually only an artefact created by the approximation.

 

[pervect]

Sorry, I've been a bit busy, and have been improving my calculations as well. Anyway, I'm now convinced of what I was starting to suspect before, which is that the "Earth frame" is a good approximation only in a region much smaller than a gravitational wavelength.

At a peak chirp frequency of 300 hz, the Ligo burst can have wavelengths as small as a million meters, or 1000 km. So it's problematical to define an rigid frame the size of the Earth, though it's not problematical to define such a frame the size of Ligo. A spheres surrounding the GW source is"right out" - it's too big for a rigid frame approximation to exist.

A rigid frame large enough to encompass "Ligo in space", outside the environment of the Earth, is not a problem at these GW frequencies though.

The math is the most convincing argument, but it gets rather technical. I'll talk about a Newtonian approach that generalizes well to a relativistic approach. This approach is to find the velocity field that represents a "material body". In 3d, the integral curves of this velocity field would be called streamlines. In the 4d case, we call the velocity field a congruence, and the integral curves of the velocity field are worldlines.

A non-rotating rigid velocity field in Newtonian mechanics has the property that the gradient of the velocity is zero. The condition for a rotating rigid congruence is only a bit harder, but I'll not address that now.

In a 3d Cartesian coordinate system [t,x,y,z] we'd write for the non-rotating rigidity condition $\frac{\partial v}{\partial x} = \frac{\partial v}{\partial y} = \frac{\partial v}{\partial z} = 0$ or $\nabla v = 0$, where $\nabla$ is the gradient operator.

The relativistic generalization of this is to write $\nabla_a u^b = 0$ where $\nabla$ is now the covariant derivative operator, and we replace the 3-velocity field v with the 4-velocity field u. One might often see this discussed in the texts with a different index position, $\nabla_a u_b$, along with a more detailed discussion of expansion, shear, and vorticity.

The result is this: using the GW metric I presented earlier, we can define a 4-velocity field so $\nabla_x u^a$ (and also $\nabla_y u^a$) have no first order terms. $\nabla_x$ is the directional derivative in the x direction of our GW coordinate system, the relativistic generalization of $\frac{\partial}{\partial x}$. By "order", I mean a series expansion in terms of what I've been calling k, which is the gravity wave amplitude. There's no sense in carrying out calculations to a higher order, the GW solution itself is only accurate to first order in k. But since k is on the order of 10^-21, it's an excellent approximation.

But it turns out (I believe the reason can be traced to the relativity of simultaneity) that when we do this, as we must to have a rigid flow, $\nabla_z u^a$ will not be zero.

Basically, we can choose our congruence to make $\nabla_x$ (and the equivalent in the y direction) zero at or near z=0, but due to the time and space variation of our metric, the choice that makes it zero at z=0 doesn't make it zero at different values of z. If we restrict the range of concern to a region of "small change in z", where the GW amplitude doesn't change much, we have a reasonable approximation to a rigid flow. If we don't restrict our range, we don't have a reasonable approximation to a rigid flow. So the shape of our almost-rigid region is more like a pancake than a sphere - it's limited to the dimension of the GW in the direction of propagation of the GW, but is large in the other two directions.

The lack of a rigid frame doesn't affect a planar Ligo out in space much at all. If we orient Ligo for maximum idealized reception, $\Delta z$ is very small, as it's perpendicular to the "long" dimensions of the apparatus. Of course, we don't have any guarantee that Ligo is oriented in this manner.

When we want to talk about the response of the Earth to the GW, we don't have a "rigid frame" to use to compute the result in. This means that we'd have to specify the material properties of the Earth, such as the Young's modulus (stiffness), and Poisson's ratio and do a very difficult calculation using non-rigid body mechanics and partial differential equations. Poisson's ratio is quantifies the fact that "when a material is compressed in one direction, it usually tends to expand in the other two directions perpendicular to the direction of compression." (quote from Wiki).

This is way too much work, and is totally irrelevant to the Ligo result anyway, because the whole purpose of the Ligo apparatus is to isolate the test masses from the environment of the Earth.

While it's a natural question to ask how the Earth responds to the GW, it looks like a hard problem to solve precisely, and I don't think I've seen anyone attempt a solution, especially since it has no experimental consequences.

Conceptually these issues wouldn't matter much to GW detection of what I've been calling "Ligo in space", because there's no problem with the size of the frame for that problem, most especially if you orient the detector optimally. Then it's easy to talk about how the test masses move relative to the beam tube, because we can approximate it in the familiar context of a rigid frame.

 

[GeorgeDishman]

Thanks for replying, the result surprises me but as I said, I'm not at all familiar with the workings of GR so this is fascinating.

At a peak chirp frequency of 300 hz, the Ligo burst can have wavelengths as small as a million meters, or 1000 km. So it's problematical to define an rigid frame the size of the Earth, though it's not problematical to define such a frame the size of Ligo.

Thank you, that is the problem I had seen albeit in my invalid approach.

.. it turns out (I believe the reason can be traced to the relativity of simultaneity) that when we do this, as we must to have a rigid flow, $\nabla_z u^a$ will not be zero.

Basically, we can choose our congruence to make $\nabla_x$ (and the equivalent in the y direction) zero at or near z=0, but due to the time and space variation of our metric, the choice that makes it zero at z=0 doesn't make it zero at different values of z. If we restrict the range of concern to a region of "small change in z", where the GW amplitude doesn't change much, we have a reasonable approximation to a rigid flow. If we don't restrict our range, we don't have a reasonable approximation to a rigid flow. So the shape of our almost-rigid region is more like a pancake than a sphere - it's limited to the dimension of the GW in the direction of propagation of the GW, but is large in the other two directions.

Yes, understood.

This is way too much work, ..

Also understood.

.. and is totally irrelevant to the Ligo result anyway, because the whole purpose of the Ligo apparatus is to isolate the test masses from the environment of the Earth.

That they are isolated is true but the range over which the isolation is effective is limited to a small fraction of a wavelength of the interferometer laser, so if the motion of the masses is too large then it will exceed the ability of the system to remain locked. That displacement limit is what I am looking at.

However, I take your point, the materials aspect makes this much more onerous so perhaps a simplified approach based on the space version might be more amenable to analysis (below).

Conceptually these issues wouldn't matter much to GW detection of what I've been calling "Ligo in space", because there's no problem with the size of the frame for that problem, most especially if you orient the detector optimally. Then it's easy to talk about how the test masses move relative to the beam tube, because we can approximate it in the familiar context of a rigid frame.

How about three copies of LIGO-in-space separated in the z direction by λ/2, would it be possible to say how that would behave? I've attached a sketch showing three tubes as black line pairs with red test masses (not to scale, λ≈2000km, tube length=4km).

Each tube individually, with its pair of masses, should be within a "pancake" region. In that view, I think the associated tubes would stretch and shrink, equivalent to the masses moving relative to the tube ends in the more usual representation. Since the tubes containing masses A-B and E-F are a wavelength apart, I am hoping we can define a congruence in which all four are always at rest and the distances A-E and B-F are also constant.
The question then is what happens to masses C and D and their associated tube? I think there should be a third "pancake region" covering them so, within that, the relative motion of the masses and tube should be as for the other two regions (just 180 degrees later), but is your calculation able to say how those two masses move relative to the congruence in which the other four are always at rest?

P.s. I'm also assuming we are simplifying by calculating for a constant wave frequency whereas the LIGO detection swept from a wavelength greater than the diameter of the Earth to 3 times smaller in less than 20ms, and that we are just working with plane waves.

 

[pervect]

How about three copies of LIGO-in-space separated in the z direction by λ/2, would it be possible to say how that would behave? I've attached a sketch showing three tubes as black line pairs with red test masses (not to scale, λ≈2000km, tube length=4km).
View attachment 103376
Each tube individually, with its pair of masses, should be within a "pancake" region. In that view, I think the associated tubes would stretch and shrink, equivalent to the masses moving relative to the tube ends in the more usual representation. Since the tubes containing masses A-B and E-F are a wavelength apart, I am hoping we can define a congruence in which all four are always at rest and the distances A-E and B-F are also constant.
The question then is what happens to masses C and D and their associated tube? I think there should be a third "pancake region" covering them so, within that, the relative motion of the masses and tube should be as for the other two regions (just 180 degrees later), but is your calculation able to say how those two masses move relative to the congruence in which the other four are always at rest?

P.s. I'm also assuming we are simplifying by calculating for a constant wave frequency whereas the LIGO detection swept from a wavelength greater than the diameter of the Earth to 3 times smaller in less than 20ms, and that we are just working with plane waves.

My gut reaction is that you could create a different congruence for each tube in the stack, but they would be slightly different, having different simultaneity conventions. So you wouldn't have a coherent picture of the whole stack sharing a single, common, convention of simultaneity.

 

[GeorgeDishman]

My gut reaction is that you could create a different congruence for each tube in the stack, but they would be slightly different, having different simultaneity conventions. So you wouldn't have a coherent picture of the whole stack sharing a single, common, convention of simultaneity.

If the assumption that the outer four masses which share the same wave phase can all be at rest at all times in this congruence, the question of simultaneity can be of lesser concern. Each of the z, y and z components of the C and D masses would, to first order, be a sine wave so all we need to characterise the motion is the three amplitudes and perhaps phases of those components. In terms of Earth-frame related limits, those amplitudes are probably a good proxy for the maximum local relative displacement. Is it possible to find out those amplitudes from your calculation? I'm sure the differential mode numbers (D relative to C etc.) are as obtained from the classic calculation but it's C relative to A and E that is of interest, especially in the X direction of course.

 

[pervect]

If the assumption that the outer four masses which share the same wave phase can all be at rest at all times in this congruence, the question of simultaneity can be of lesser concern.

I don't see how, but perhaps we're not viewing the problem the same way at all.

What we want to do is measure fractional distance changes on the order of 10^-21 or so of, say, 3km or so. That's about 3*10^-18 meters, which, if we use relativistic methods to measure the distance based on light propagation, demands synchronization accuracies on the order of 10^-26 seconds over that 3km region.

So we wind up having to worry about non-intuitive seemingly very small effects due to the relativity of simultaneity if we wish to use relativistic based methods to measure the distance.

Perhaps you have some other idea of how to measure distance at the back of your mind? I can't really say, but I can say that if you want to compare whatever method, notion, or definition of distance you might have in mind to relativistic based method based on light travel time, you'll need synchronizations of the stated accuracy to do it in a meaningful manner.

And a lot of the mathematics has been in support of determining the theoretical existence of rigid congruences with the necessary syncrhonization accuracies.

One way of viewing the whole congruence issue is as of a means to specify a synchronization convention. "Specifying an synchronziation convention" sounds rather abstract, but physically specifying one specifies the other.

On a somewhat related note, it's perfectly reasonable to use non-rigid congruences to measure distances, but you'll get different results than you do if you use rigid ones. The "expanding space" point of view in fact does use non-rigid congruences to define distances, and it turns out to not make much difference. But in order to determine that it doesn't make any difference, it's helpful to compare the distance measured by a rigid congruence to the distance measured by a non-rigid one. But in order to do that, first one needs a rigid congruence to exist in the first place, otherwise you don't have anything to compare against. Fortunately, in this problem, the needed congruence does exist over a useful region.

 

[RockyMarciano]

On a somewhat related note, it's perfectly reasonable to use non-rigid congruences to measure distances, but you'll get different results than you do if you use rigid ones. The "expanding space" point of view in fact does use non-rigid congruences to define distances, and it turns out to not make much difference. But in order to determine that it doesn't make any difference, it's helpful to compare the distance measured by a rigid congruence to the distance measured by a non-rigid one. But in order to do that, first one needs a rigid congruence to exist in the first place, otherwise you don't have anything to compare against. Fortunately, in this problem, the needed congruence does exist over a useful region.

I think you are getting too far away from what is mathematically meaningful here. At least I'm not aware of any notion of "non-rigid" congruence in Pseudo-Riemannian geometry. Congruences in general are just integral curves defined by vector fields, perfectly rigid and nothing changes in the GR case of spacelike congruences.