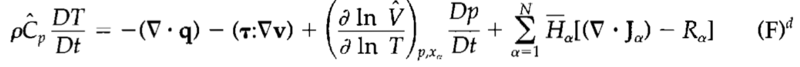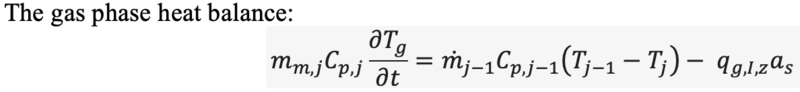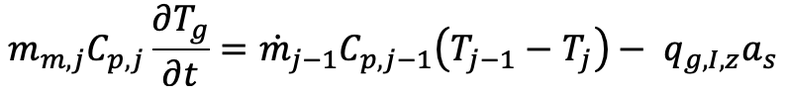Modelling of two phase flow in packed bed (continued)

[casualguitar]

This has nothing to do with composition. It says that the total number of moles exiting the tank per unit time is equal to the total number of moles per unit time entering minus the rate of change in the number of moles as a result of the rate of temperature increase at constant pressure, and minus the molar rates of solid- and liquid deposition onto the bed.

Agreed that this is unrelated to composition. However we mentioned earlier that we're not tracking composition changes in the gas phase so would this exiting molar flow technically be of the same composition as the inlet flow. Yes we will lose some of each component to the solid phase, however is it correct to say we assume that this does not affect the gas phase composition?

You realize that there are 6 times the number of tanks number of coupled ODEs being solved, right? This involves the solution of 6 times the number of tanks non-linear algebraic equations being solved at each time step.

So we have 6 ODEs here, and 2 ODEs in the last model, would that be 3 times the number of ODEs being solved? Or am I missing something? But yes it does seem like this could add significantly to the computation time. That said, we don't need thermo to calculate T(H,P) or the density/enthalpy derivative. I think these were quite costly so hopefully this balances out somewhat.

I guess you can start out by assuming constant values for the heat transfer coefficients and mass transfer coefficients. The actual coding for these could be added later within the derivative determination subroutine.

Agreed yes I think constant U, mass transfer coefficient and even constant Cp just to see how the code for this will look. Will start coding on this system tomorrow morning!

 

[Chestermiller]

Agreed that this is unrelated to composition. However we mentioned earlier that we're not tracking composition changes in the gas phase so would this exiting molar flow technically be of the same composition as the inlet flow. Yes we will lose some of each component to the solid phase, however is it correct to say we assume that this does not affect the gas phase composition?

This is included in the overall molar balance. No assumptions are made about the composition of the molar flux.

So we have 6 ODEs here, and 2 ODEs in the last model, would that be 3 times the number of ODEs being solved?

Sure

Agreed yes I think constant U, mass transfer coefficient and even constant Cp just to see how the code for this will look. Will start coding on this system tomorrow morning!

The equation F in BSL table 19.2-4 and Exercise 19D.2 seem to suggest that Cp should be evaluated at the existing overall molar composition as $\sum{y_iC_{P,i}}$.

I should also point out that, in BSL, the molar flux is defined in terms of the mass transfer coefficient by $$\dot{M}_i^"=k_i\left(y_i-\frac{p_i(T)}{P}\right)$$ where $k_i$ has units of moles/m^2s. Under these definitions, the Sherwood number for a porous medium (for use in conjunction with the correlation equation) would be defined as $$\frac{k_iD_p}{(1-\epsilon)cD_i\psi}$$ where, in BSL notation, $$c=\rho_{m}=\frac{P}{RT_I}$$

BSL point out that $cD_i$ is much less dependent on temperature than $D_i$.

 

[casualguitar]

This is included in the overall molar balance. No assumptions are made about the composition of the molar flux.

Sorry yes I understand now

The equation F in BSL table 19.2-4 and Exercise 19D.2 seem to suggest that Cp should be evaluated at the existing overall molar composition as ∑yiCP,i.

Ok can do, this seems easy enough to implement anyway.

I could use the tank j-1 position composition to evaluate Cp at tank j as $\sum{y_iC_{P,i}}$. But yes for now I'll leave it constant to simplify, unless there is a reason not to do this. I'd like to solve the ODEs with as little 'surrounding calculations' as possible

I should also point out that, in BSL, the molar flux is defined in terms of the mass transfer coefficient by M˙i"=ki(yi−pi(T)P) where ki has units of moles/m^2s. Under these definitions, the Sherwood number for a porous medium (for use in conjunction with the correlation equation) would be defined as kiDp(1−ϵ)cDiψ where, in BSL notation, c=ρm=PRTI

BSL point out that cDi is much less dependent on temperature than Di.

Understood. I'll switch to this approach then for the mass transfer coefficient function

So in summary for this iteration of this model:

Two mole balances (H2O and CO2):

Two solid phase balances (H2O and CO2):

One gas phase and one bed heat balance:

I am tempted to avoid using pythons thermo as much as possible here so save on computation cost and also confusion regarding the solid phase. I think given that thermo can't 'see' the solid phase it will cause some issues down the line so it might be best here to define some other curves manually rather than having to deal with the thermo black box:
- The gas phase N2, H2O and CO2 density curves
- The ideal gas heat capacity curves for N2, H2O and CO2

Is this reasonable?

The only place we will need nitrogen data is in the gas phase heat balance is this correct?

Also we can leave out the CO2 condensation curve completely as we're not in a pressure range that would allow this to occur

As constant in this first iteration of the model (just solving the ODEs really for now) could be the ideal gas heat capacity values, the mass transfer coefficient, component densities, and the heat transfer coefficients

Lastly the initial and boundary conditions are:

ICs:
- molar holdup of H2O and CO2 (both zero initially)
- bed temperature
- gas temperature (= bed temperature)
- mole fractions of H20 and CO2 (both zero initially)

BCs:
- molar flow of each component into the bed
- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

Does the above look reasonable to you?

 

[Chestermiller]

Sorry yes I understand now

Ok can do, this seems easy enough to implement anyway.

I could use the tank j-1 position composition to evaluate Cp at tank j as $\sum{y_iC_{P,i}}$.

No. These are at the j position. In the derivative subroutine coding for the j'th tank, the solution vector has values for the y's in the j'th tank.
No. Let the automatic integrator do it all for you.

Understood. I'll switch to this approach then for the mass transfer coefficient function

So in summary for this iteration of this model:

Two mole balances (H2O and CO2):
View attachment 300204
Two solid phase balances (H2O and CO2):
View attachment 300207
One gas phase and one bed heat balance:
View attachment 300209
View attachment 300208

- The gas phase N2, H2O and CO2 density curves
- The ideal gas heat capacity curves for N2, H2O and CO2

You're not going to have N2 condense, are you? Why do you need the gas phase densities of the N2, H20, and CO2.

Is this reasonable?

The only place we will need nitrogen data is in the gas phase heat balance is this correct?

Why do we need it in the gas phase heat balance. The molar density of the gas phase is P/RT, where P is the total pressure.

Also we can leave out the CO2 condensation curve completely as we're not in a pressure range that would allow this to occur

Correct.

As constant in this first iteration of the model (just solving the ODEs really for now) could be the ideal gas heat capacity values, the mass transfer coefficient, component densities, and the heat transfer coefficients

Lastly the initial and boundary conditions are:

ICs:
- molar holdup of H2O and CO2 (both zero initially)
- bed temperature
- gas temperature (= bed temperature)
- mole fractions of H20 and CO2 (both zero initially)

BCs:
- molar flow of each component into the bed

Just total molar flow and mole fractions. Tuinier uses mole fractions.

- mole fraction of each component into the bed (or we can calculate this from the above)
- temperature of the flow into the bed

Does the above look reasonable to you?

Yes.

 

[casualguitar]

No. These are at the j position. In the derivative subroutine coding for the j'th tank, the solution vector has values for the y's in the j'th tank.
No. Let the automatic integrator do it all for you.

Ok I don't fully understand yet how we can use j position composition values to calculate j position Cp values. I guess this is possible with implicit integrators however I don't have a picture of how this works in my head yet. Will be reading the documentation soon

You're not going to have N2 condense, are you? Why do you need the gas phase densities of the N2, H20, and CO2.

No N2 condensation, however if we're calculating the mass holdup in the heat balance then I thought we would calculate this with density correlations for each of N2,CO2 and H2O however as you have said we can use P/RT here

Just total molar flow and mole fractions. Tuinier uses mole fractions.

Got it, total molar flow and mole fractions, as these will give us the individual component flows of CO2 and H2O for the mass balances

Yes.

Ok great

 

[casualguitar]

Hi Chet, just letting you know I was sidetracked by some other work. Will be back on the ODE code tomorrow morning

 

[casualguitar]

Hi Chet, just letting you know I was sidetracked by some other work. Will be back on the ODE code tomorrow morning

Hi Chet, just updating - working on the code now. I didn't really understand what I was doing first time around with regards to using the ODE solver to solve position dependent ODEs, so I'm taking my time on it this time around i.e. I understand how to use the integrator to solve ODEs where there is no spatial discretisation, but adding in spatial discretisation from the coding point of view is difficult

 

[Chestermiller]

Hi Chet, just updating - working on the code now. I didn't really understand what I was doing first time around with regards to using the ODE solver to solve position dependent ODEs, so I'm taking my time on it this time around i.e. I understand how to use the integrator to solve ODEs where there is no spatial discretisation, but adding in spatial discretisation from the coding point of view is difficult

Not really. Discretizing with respect to the position variable z reduces the equations from a set of PDEs to a set of ODEs. This is the Method of Lines.

 

[Chestermiller]

The solution vector consists of a single column vector containing the values of all the time-integrated variables in all the tanks. When you use an automatic integrator, you furnish the integrator with a subroutine which has the solution vector in its calling sequence and which has the coding for mapping the solution vector into a column vector of the time-derivative of the solution vector.

In such a subroutine, I would start out by decomposing the solution vector into the temperatures, mole fractions, and amounts of deposits in the tanks using meaningful tank-indexed parameters like T's, y's, and M's. Then, I would calculate the time derivatives of these using our balanced equations, in terms of dT/dt's, dy/dt's, and dM/dt's. Then I would remap (recompose) these into a single time derivative column vector.

I hope this makes sense.

 

[casualguitar]

The solution vector consists of a single column vector containing the values of all the time-integrated variables in all the tanks. When you use an automatic integrator, you furnish the integrator with a subroutine which has the solution vector in its calling sequence and which has the coding for mapping the solution vector into a column vector of the time-derivative of the solution vector.

In such a subroutine, I would start out by decomposing the solution vector into the temperatures, mole fractions, and amounts of deposits in the tanks using meaningful tank-indexed parameters like T's, y's, and M's. Then, I would calculate the time derivatives of these using our balanced equations, in terms of dT/dt's, dy/dt's, and dM/dt's. Then I would remap (recompose) these into a single time derivative column vector.

Yep this makes complete sense. It is setting up the various arrays in such a way that it is possible/easy to remap them that it difficult (the mass balances are dependent on the number of species but the heat balances are not so it seems to make setting up this subroutine a bit awkward). I will post my pseudocode for this today

 

[Chestermiller]

Please, first show me what your tentative layout of the solution vector looks like.

 

[casualguitar]

Just some questions on the mass flow out of a tank equation:

This term has a time derivative on the RHS. Is it correct to say that:
1) The time derivative term in this equation comes from solving the gas phase heat balance for $\frac{\partial T_g}{dt}$ and subbing it in here?
2) We will not be including this equation in the integration itself, but just using it to link the flows between tanks

 

[Chestermiller]

Just some questions on the mass flow out of a tank equation:
View attachment 300643
This term has a time derivative on the RHS. Is it correct to say that:
1) The time derivative term in this equation comes from solving the gas phase heat balance for $\frac{\partial T_g}{dt}$ and subbing it in here?

Yes, the heat balance for tank j.

2) We will not be including this equation in the integration itself, but just using it to link the flows between tanks

Yes. It is the last thing you calculate before moving on to calculate the derivatives for the next tank.

 

[casualguitar]

Yes, the heat balance for tank j.

Yes. It is the last thing you calculate before moving on to calculate the derivatives for the next tank.

Just commenting to say I'm still working on the code. Should have pseudocode by tomorrow

 

[casualguitar]

Just commenting to say I'm still working on the code. Should have pseudocode by tomorrow

Hi Chet, yet another update from me that I am still working on the code (other things came up like experimental work, moving house etc also)

 

[casualguitar]

Hi Chet, yet another update from me that I am still working on the code (other things came up like experimental work, moving house etc also)

Just to fill you in slightly on where I'm at - I am trying to set up two functions that set up the ODEs for:
1) the initial/boundary conditions
2) the rest of the system

Here is the function for 'the rest of the system'. Note I have left some non constants as constants just because this is really pseudocode i.e. getting the structure right

I should do something similar for the initial/boundary conditions, however I'm a bit stuck as for how to split up the boundary and initial conditions. Working on it though. For reference here is the current 'initial ODE system' code which sets up the ODEs at t=0 which may not make much sense currently:

Working on it

 

[casualguitar]

Yes, the heat balance for tank j.

Yes. It is the last thing you calculate before moving on to calculate the derivatives for the next tank.

Hey Chet, hope alls well with you.

My apologies, I'm really struggling to set up these initial/boundary conditions. I have found effectively no examples online of solve_ivp being used in this way.

Is it reasonable to implement a simple explicit Euler instead here? I might have to play with the dt depending on the systems stiffness but it would give a first solution. Maybe not too accurate but we could go from there

Are there any big reasons to stick with the automatic integrator?

 

[casualguitar]

Hey Chet, hope alls well with you.

My apologies, I'm really struggling to set up these initial/boundary conditions. I have found effectively no examples online of solve_ivp being used in this way.

Is it reasonable to implement a simple explicit Euler instead here? I might have to play with the dt depending on the systems stiffness but it would give a first solution. Maybe not too accurate but we could go from there

Are there any big reasons to stick with the automatic integrator?

Just posting the updates we had over private message -
- boundary condition issues solved
- working on the property/dimensionless number functions

Question:
Just doing the $h_{fs}$ function currently which takes $Pr$, $Re$ and $k_g$ as inputs.

For the $k_g$ value, is it reasonable to use a mole fraction averaged $k_g$ value here? I.e. take the feed mole fractions of CO2, H2O and N2, calculate $k_g$ of each at the given temperature and then return a mole fraction weighted $k_g$ value?

Edit: This would mean I should write correlation functions for N2 also (cp, mu, rho, etc). I have avoided that up until now because N2 is not present in the ODEs

Edit2: Is it also correct to say that $h_{fs}$ is completely independent of the solid properties?

 

[Chestermiller]

Just posting the updates we had over private message -
- boundary condition issues solved
- working on the property/dimensionless number functions

Question:
Just doing the $h_{fs}$ function currently which takes $Pr$, $Re$ and $k_g$ as inputs.
View attachment 301632

Where is the Dp?

For the $k_g$ value, is it reasonable to use a mole fraction averaged $k_g$ value here? I.e. take the feed mole fractions of CO2, H2O and N2, calculate $k_g$ of each at the given temperature and then return a mole fraction weighted $k_g$ value?

This is only going to be approximate. In any event, BSL gives mixing rules for k.

Edit: This would mean I should write correlation functions for N2 also (cp, mu, rho, etc). I have avoided that up until now because N2 is not present in the ODEs

This doesn't seem like a big deal.

Edit2: Is it also correct to say that $h_{fs}$ is completely independent of the solid properties?

Of course.

 

[casualguitar]

Where is the Dp?

Typo (this was included in the previous model)

This equation returns $h_{fs}$ values in the $200-1000W/m2K$ range for typical Reynolds numbers (up to $10^4$)

This doesn't seem like a big deal.

Yes its not

Of course.

Nice. Except for the particle diameter I suppose if that is considered to be a solid property

Anyway I'm almost there with these functions. I think I'll post plots of them all with typical dependent variable ranges just to confirm they're all working as expected before moving on.

For reference, the plots will roughly include:

 

[casualguitar]

For the mass transfer coefficient, I'm confused regarding the reason we need to calculate the Sherwood number. Heres the flow currently:

So we calculate the Re and Sc numbers. Then the mass transfer coefficient $k_i$ seems to be a function of just these two numbers, so why the need to calculate the Sherwood number? And is Sh actually equal to $k_f$?

 

[casualguitar]

So I worked back through the mass transfer coefficient correlation derivation (my post above was a load of nonsense in hindsight, apologies). I almost have it but have uncertainty about which Sh number correlation to use. Heres the derivation (I just read back over the heat transfer coefficient derivation you did as its analogous to the mass transfer coefficient):

1) Define Sc and Re
$Re = \frac{6G_0}{a\mu\Psi}$
$Sc = \frac{\mu}{\rho D}$

2) Define the sherwood number
$Sh = \frac{k_id_p}{\rho_mD_{ab}}$

I took this one from BSL. I know you defined another Sh number earlier which was:
$Sh_{loc,i}=\frac{k_iD_p}{(1-\epsilon_g)D_i\psi}$

Its easy to interchange between the two but I am not sure of the reason to use one over the other

Anyway

3) Defining the CC factor $j_D$ as:
$j_D = ShRe^{-1}Sc^{-1/3}$

4) And the same specifically for packed beds:
$j_D = 2.19Re^{-2/3} + 0.78Re^{-0.381}$

5) Letting 3 equal to 4 and solving for k_i:
$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{a,b}\frac{\rho}{d_p}$

Is this correct? I can easily sub in your Sh number instead of the BSL one, but what is the reason you did not use the BSL one?

 

[Chestermiller]

So I worked back through the mass transfer coefficient correlation derivation (my post above was a load of nonsense in hindsight, apologies). I almost have it but have uncertainty about which Sh number correlation to use. Heres the derivation (I just read back over the heat transfer coefficient derivation you did as its analogous to the mass transfer coefficient):

1) Define Sc and Re
$Re = \frac{6G_0}{a\mu\Psi}$
$Sc = \frac{\mu}{\rho D}$

2) Define the sherwood number
$Sh = \frac{k_id_p}{\rho_mD_{ab}}$

I took this one from BSL. I know you defined another Sh number earlier which was:
$Sh_{loc,i}=\frac{k_iD_p}{(1-\epsilon_g)D_i\psi}$

Its easy to interchange between the two but I am not sure of the reason to use one over the other

Anyway

3) Defining the CC factor $j_D$ as:
$j_D = ShRe^{-1}Sc^{-1/3}$

4) And the same specifically for packed beds:
$j_D = 2.19Re^{-2/3} + 0.78Re^{-0.381}$

5) Letting 3 equal to 4 and solving for k_i:
$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{a,b}\frac{\rho}{d_p}$

Is this correct? I can easily sub in your Sh number instead of the BSL one, but what is the reason you did not use the BSL one?

The approach I'm recommending is based on Reynolds analogy, and I think it is better. I don't think that BSL considered this.

I believe your eon 5 is correct if dp is calculated by the definition in BSL.

 

[casualguitar]

The approach I'm recommending is based on Reynolds analogy, and I think it is better. I don't think that BSL considered this.

I believe your eon 5 is correct if dp is calculated by the definition in BSL.

Hmm I'm taking the characteristic length from the Sherwood number $l_0$ to be $d_p$, the particle diameter. Why would dp be calculated using the BSL definition? Or have I misunderstood. The units for $k_i$ I have are $mol/m2.s$ not $m/s$ so I guess I am mistaken somewhere here

Also I'm effectively finished the function write ups and plots. I have the mass transfer coefficient one to confirm correct, then the mass deposition one is built on this so I have that also. Besides that I have two small questions regarding $U_b$ and $U_g$

So $U_b$ will be a constant times the thermal conductivity divided by the particle diameter. This constant is $\beta$ I presume, which is equal to 10 for spheres, meaning that we would get $U_b = \frac{\beta k_p}{d_p}$?

For $U_g$ we can evaluate this at the bulk gas temperature. I have taken the exact same correlation as we had in the previous model. However you mentioned we would have a correction factor involving viscosity at the interface this time? Why would we have this?

 

[Chestermiller]

Hmm I'm taking the characteristic length from the Sherwood number $l_0$ to be $d_p$, the particle diameter. Why would dp be calculated using the BSL definition? Or have I misunderstood. The units for $k_i$ I have are $mol/m2.s$ not $m/s$ so I guess I am mistaken somewhere here

I had this worked out a few weeks ago, but don't quite remember now. You need to look at the table in BSL that has various versions of this in there. If I remember correctly, it is almost certainly the $mol/m2.s$ that we should be using. You need to play with the different versions until you arrive at the one that makes sense to you.

Also I'm effectively finished the function write ups and plots. I have the mass transfer coefficient one to confirm correct, then the mass deposition one is built on this so I have that also. Besides that I have two small questions regarding $U_b$ and $U_g$

So $U_b$ will be a constant times the thermal conductivity divided by the particle diameter. This constant is $\beta$ I presume, which is equal to 10 for spheres, meaning that we would get $U_b = \frac{\beta k_p}{d_p}$?

Yes, I think so.

For $U_g$ we can evaluate this at the bulk gas temperature. I have taken the exact same correlation as we had in the previous model. However you mentioned we would have a correction factor involving viscosity at the interface this time? Why would we have this?

See BSL section on heat transfer for turbulent flow in a pipe.

 

[casualguitar]

The approach I'm recommending is based on Reynolds analogy, and I think it is better. I don't think that BSL considered this.

I believe your eon 5 is correct if dp is calculated by the definition in BSL.

Ok got it I think. So using BSLs Sherwood number is ok, however the Reynolds analogy approach you used is better, meaning that $k_i$ would go from this with the BSL Sherwood number of $Sh_{loc,i} = \frac{k_id_p}{\rho_mD_{ab}}$:
$$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}D_{a,b}\frac{\rho}{d_p}$$

To this, with your Sherwood number of $Sh_{loc,i}=\frac{k_id_p}{(1-\epsilon_g)D_i\psi}$:
$$k_i = (2.19Re^{1/3} + 0.78Re^{0.619})Sc^{1/3}(1-\epsilon_g)D_i\frac{\psi}{d_p}$$

How would I assess which Sh correlation is better? I could plot one against the other for a range of $k_i$ values and see if they are almost equivalent. However if one returns appreciably higher values than the other I am not sure how to assess which is the better of the two

 

[casualguitar]

You need to play with the different versions until you arrive at the one that makes sense to you.

Yes any version I have tried has produced $mol/m^2.s$ so I'll go with this for now unless I see an inconsistency

Yes, I think so.

See BSL section on heat transfer for turbulent flow in a pipe.

Great, will do that this morning

Edit: Found those correlations. They give the laminar (Re<2100) and highly turbulent flow equations (Re>20000). The transition flow region is only available from a graph (no equation provided I don't think). The Re number for this system seems to be in the region of 20000 or so anyway, so for simplicity I will take the turbulent flow equation rather than extracting the relevant equation from the graph. That equation for forced convection and turbulent flow in tubes (and L/D > 10) is:
$$Nu_{ln} = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}$$
where $\mu_b$ is the bulk viscosity and $\mu_0$ is the surface viscosity which are I guess evaluated at the solid and fluid temperatures respectively?

So, this would mean the new $U_g$ heat transfer coefficient would be:
$$U_g = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}\frac{k_g}{d_p}$$

For reference, the previous model HTC was:
$$U_g = (2.19Re^{1/3} + 0.78Re^{0.66})Pr^{1/3}\frac{k_g}{d_p}$$

 

[casualguitar]

Lastly, regarding the units of ki, any equation with ki in it shows that the unit of ki is $mol/m^2.s$. However, the molar desublimation rate formula $\dot{M}_i^"=k_i\left(\frac{Py_i-p_i(T_I)}{RT_I}\right)\tag{1}$ suggests that the units are $m/s$. If this is correct, is there an equivalent molar desublimation rate equation that would use units of mol/m2.s for ki?

For reference, my units are:
$k_i$ = $mol/m^2.s$
$P$ = $Pa$
$y_i$ = $mol/mol$
$R$ = $J/mol.K$
$T$ = $K$

 

[Chestermiller]

Yes any version I have tried has produced $mol/m^2.s$ so I'll go with this for now unless I see an inconsistencyGreat, will do that this morning

Edit: Found those correlations. They give the laminar (Re<2100) and highly turbulent flow equations (Re>20000). The transition flow region is only available from a graph (no equation provided I don't think). The Re number for this system seems to be in the region of 20000 or so anyway, so for simplicity I will take the turbulent flow equation rather than extracting the relevant equation from the graph. That equation for forced convection and turbulent flow in tubes (and L/D > 10) is:
$$Nu_{ln} = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}$$
where $\mu_b$ is the bulk viscosity and $\mu_0$ is the surface viscosity which are I guess evaluated at the solid and fluid temperatures respectively?

So, this would mean the new $U_g$ heat transfer coefficient would be:
$$U_g = 0.026Re^{0.8}Pr^{1/3}\frac{\mu_b}{\mu_0}^{0.14}\frac{k_g}{d_p}$$

For reference, the previous model HTC was:
$$U_g = (2.19Re^{1/3} + 0.78Re^{0.66})Pr^{1/3}\frac{k_g}{d_p}$$

No. No. The correlation you chose is for flow in a pipe, not a packed bed. You should continue to use the packed bed correlation, but just apply the wall viscosity correction.

 

[casualguitar]

No. No. The correlation you chose is for flow in a pipe, not a packed bed. You should continue to use the packed bed correlation, but just apply the wall viscosity correction.

Ah ok so it would be $U_{g,NEW} = U_{g,OLD}*\frac{\mu_b}{\mu_0}^{0.14}$?