Moment of Inertia Problems and Conservation of Energy

[Lancelot59]

I have this situation here:

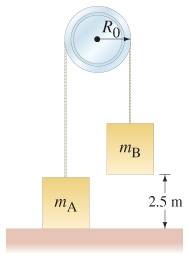
I'm given the masses for the objects, as well as the radius and mass of the pulley. I have to use conservation of energy laws to find out how fast the mass on the right is going the instant it hits the ground.

I can find out what the alpha of the pulley is, and therefore the accelration of the system, but that's just kinematics. How can I use conservation of energy to do it?

How could I do it if the pulley was ideal?

 

[Doc Al]

How can I use conservation of energy to do it?

Compare the total mechanical energy of the system before and after the mass falls.

 

[Lancelot59]

I don't follow...

I see that there is none before, and some after, when the block b has zero potential energy, block A has potential and kinetic energy, and the pulley has rotational kinetic energy...but if I knew those values then I could just save the trouble and use kinematics.

 

[Doc Al]

Set up a conservation equation:
KE₁ + PE₁ = KE₂ + PE₂

Make sure you include the PE and KE of both masses and the pulley. You'll be able to solve for the speed of block B without using force equations or kinematics. Hint: Express all the KE terms in terms of the speed of block B.