Momentum and Angular Velocity Question

[zorro]

Homework Statement

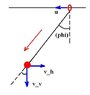
A ring of mass m free to slide on a fixed smooth horizontal wire is attached to one end of a string of length 60cm. The other end of the string is attached to a particle of mass 2m. The ring and the particle are initially held at the same horizontal level with the string taut. If the system is now released, find the angular velocity of the string when it makes an angle of 60 degrees with the vertical.

Homework Equations

conservation of momentum and energy

The Attempt at a Solution

When the string makes an angle 60 degrees with the vertical,
momentum in horizontal direction is conserved...
2mv=mu
i.e. u=2v...where v is the horizontal component of velocity of mass 2m
I am not getting the concept after this. Please help

 

[hikaru1221]

Does the problem mention anything about the ring's radius?

 

[zorro]

No, nothing is mentioned about it.
I guess it is negligible

 

[hikaru1221]

Okay, then I guess the problem implies that initially the mass is held at the same height as the ring such that the string is along the wire. Correct? If so then here are some hints:
_ The mass's velocity has 2 components: horizontal v_h and vertical v_v. From the momentum conservation law, you can find the relation between the ring's speed u and v_h.
_ There is a geometric restriction: the string must always be stretched, i.e. the distance between the ring and the mass is constant. That means, the projection of ring's velocity on the string = the projection of the mass's velocity on the string. From this condition, you can find the relation between u, v_h and v_v.
_ The 3rd equation is the energy conservation equation.
You have 3 equations with 3 unknowns ---> solvable, right?

 

[zorro]

Sir,
I got the first and last hints...
but in the second one, the direction of the velocity of mass is perpendicular to the string at every instant during its motion i.e. it has no component along the string ( as it is perpendicular )...please clear this

 

[hikaru1221]

Sir,

Eek, I'm not that old to be called "sir"

I got the first and last hints...
but in the second one, the direction of the velocity of mass is perpendicular to the string at every instant during its motion i.e. it has no component along the string ( as it is perpendicular )...please clear this

This is where you got it wrong (the bold part). Only when the mass performs a circular motion is its velocity perpendicular to the string. But that's not this case. Because the ring also moves, the mass is not in circular motion.

To go from the root, actually that "the velocity of mass is perpendicular to the string at every instant during its motion in circular motion" also come from the same geometric restriction: The length of the string, or more exactly, the distance between the mass and the center is constant. Because the center in circular motion is fixed, its velocity is zero, which means its component along the string is also zero. In order to satisfy the restriction, the component along the string of the mass's velocity must also be zero.

(But this is true only when the string is stretched, i.e. the distance between mass & center is fixed. Otherwise, the restriction is broken)

 

[zorro]

lol...ok I will call u bro.
Can u just derive the equation of second hint? I still have some difficulty in it.

 

[hikaru1221]

Along the string (the red arrow):
_ Component of ring's velocity: $$usin\phi$$
_ Component of the mass's velocity: $$v_vcos\phi-v_hsin\phi$$
The restriction leads to: $$usin\phi=v_vcos\phi-v_hsin\phi$$ at all time.

 

[zorro]

Thanks a lot bro...that really helped :)