More tension in a wire attached to a rod

[hooper.d]

Homework Statement

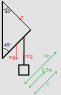
A 7.1 kg rod of 1.00 m in length is hinged to a vertical wall and supported by a thin wire. The wire and rod each make angles of 45° with the vertical. When a 10.0 kg block is suspended from the midpoint of the rod, the tension T in the supporting wire is 59 N. If the wire will break when the tension exceed 86 N, what is the maximum distance from the hinge at which the block can be suspended?

Homework Equations

Equilibrium equations

The Attempt at a Solution

?

 

[cupid.callin]

you need to provide the figure
i can't figure out there is the wire attached to ... vertical of horizontal wall

 

[hooper.d]

oh, right. sorry. here is the image.

 

[cupid.callin]

i recommend using rotation ...

torque due to weight = torque due to wire

find it in terms of distance of 10kg from hinged point
and put max tension as 86N

 

[hooper.d]

what would the equation for torque due to weight be in this case?

 

[cupid.callin]

find the distances and put values ... torque due to weight of rod + torque due to weight of block = torque due to tension

and in this case T would be ____ ??

remember mag of torque is force x perpendicular distance b/w line of force and point about which you are finding force