Ticklez_Panda
- 6
- 0
The figure below shows a velocity versus time plot for two objects; they are at the same point at
t = 0.
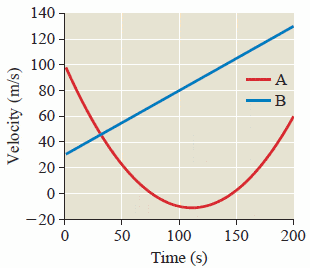
Do the objects ever have the same displacement? If so, when does that happen?
Δd = ((velocityi+ velocityf) / 2) Δt
acceleration = change in velocity / change in time
Δd(A) = 100Δt + 0.5 (accel. Δt^2)
Δd(B) = 30Δt + 0.5 (accel. Δt^2)
Looking at the graph, I can tell that line:B has a constantly changing velocity and therefore a constant acceleration. Line:A is different, it resembles a quadratic and displays the characteristic of a non-constant (time dependent acceleration). I know that the displacement between the two lines will be the same when the sum of initial and final velocity are equal given by my displacement equation.
Could someone please help to guide me towards this solution? It seems incredibly simple but I just can't grasp it. :(
t = 0.
Homework Statement
Do the objects ever have the same displacement? If so, when does that happen?
Homework Equations
Δd = ((velocityi+ velocityf) / 2) Δt
acceleration = change in velocity / change in time
Δd(A) = 100Δt + 0.5 (accel. Δt^2)
Δd(B) = 30Δt + 0.5 (accel. Δt^2)
The Attempt at a Solution
Looking at the graph, I can tell that line:B has a constantly changing velocity and therefore a constant acceleration. Line:A is different, it resembles a quadratic and displays the characteristic of a non-constant (time dependent acceleration). I know that the displacement between the two lines will be the same when the sum of initial and final velocity are equal given by my displacement equation.
Could someone please help to guide me towards this solution? It seems incredibly simple but I just can't grasp it. :(
Last edited: