Motorcycle model and tire force

[LucaCaiaffa]

I'm having issues in the application of tire forces while deriving a multi-body model of a motorcycle via Lagrange.

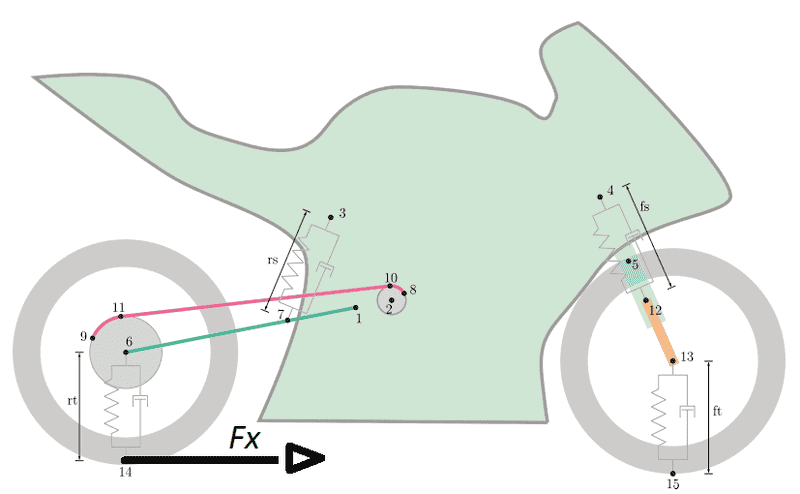
In particular, I considered several bodies that are: swingarm, main frame,
front upper fork, front lower fork and wheels.

I suppose the wheels to have zero slippage, then knowing the wheel rear torque
as $T$ and the rear radius as $R_r$ we have that $F_x=T/R_r$

The kinematic model is correct and also forces from suspensions (the model
have been validated).The problem arises from the application point of $F_x$.
While calculating the generalized force from $F_x$ the rear radius disappear,
meaning that the applied force acts like if it is applied in the center of the rear wheel instead of the contact point of the tire.

This results in same vehicle acceleration but different applied torques, but i don't know how to handle this issue.

I saw that many models found the same problem, but i don't get the point why this appears.

Thank you for your support

 

[Lnewqban]

The represented force points in the wrong direction.
The pavement-tire contact patch is the fulcrum of a lever.
The chain applied force is at top of the rear sprocket, the reaction force is applied to the axis of the tire, which moves forward, pushing the chassis via swingarm.

 

[jack action]

While calculating the generalized force from $F_x$ the rear radius disappear

What do you mean by "it disappears"?

The represented force points in the wrong direction.

No, it's not if it is the reaction force from the ground acting on the motorcycle.

 

[LucaCaiaffa]

What do you mean by "it disappears"?

I mean that there is no difference in applying the longitudinal tire force in the contact point or in the wheel hub.

This happens because no generalized coordinates relates the wheel hub and the tire contact point, and their jacobians for computing the generalized forces result the same.

For this reason I think I am "losing" a torque contribution in doing this.

Simplifying the problem, if i consider the motorcycle as a unique rigid body, I should have a torque contribution from the longitudinal force as $T=F_xh$ where $h$ is the height of the center of mass.

My model instead seems to lose the radius from the height of center of mass.

 

[jack action]

We will need to see your equation to help you further.

This happens because no generalized coordinates relates the wheel hub and the tire contact point,

I don't have real experience with the Lagrange equation, but can't you include the rotational wheel mass and angular velocity? The wheel angular displacement $\theta$ does relate to the motorcycle displacement $x$ with $x= \theta R_r$.

 

[berkeman]

It sounds like your equations are not quite right yet for the model, even with the bike upright? Is your goal to extend the model to the bike while it is leaned over in a turn? And then adding in rear tire slippage?

https://external-preview.redd.it/Vg...bp&s=bdd81c541901872cf2df7bb1aedd10a05529b84e