kostoglotov
- 231
- 6
I have what I think is a valid solution, but I'm not sure, and when I try to check the answer approximately in Matlab, I don't get a verified value, and I'm not sure if my analytic solution or my approximation method in Matlab is at fault.
1. Homework Statement
Evaluate the integral
\int_0^1 \int_0^1 e^{max(x^2,y^2)}dydx
where max(x^2,y^2) is the larger of the numbers x2 and y2.
Assumption: I'm assuming that x2 and y2 are real valued.
I consider the region of integration thusly
There is symmetry about the line y = x. Below this line, the max value is of y squared, since for y < x, y2 > x2. And so above the line y = x, the max value is x squared.
This is true because 0 <= x <= 1 and 0 <= y <= 1.
Using Matlab to sketch the 3-D graph gets
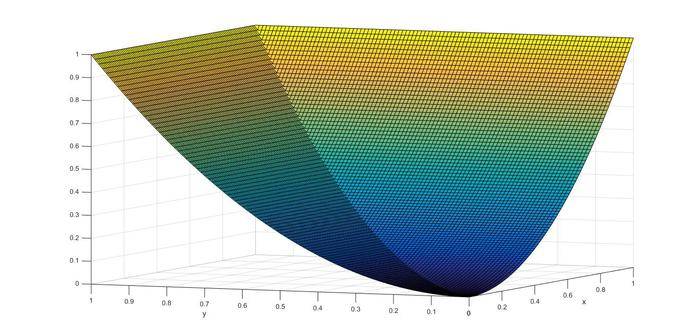
This looks right, and we can see the symmetry.
Now, if we setup the region is that we just integrate over the triangle created by y=x dividing the square [0,1]x[0,1], knowing that we must multiply the result by 2 at the end, we could evaluate the integral
\int_0^1 \int_0^x e^{y^2} dy dx
Now, this is problematic, since we can't eval. this analytically.
We can change the order of integration, but this results in further evariable squared integrated with respect to said variable situations. For instance, in one arrangement we get
\int_0^1\int_x^1 e^{x^2} dy dx
inner integral
\int_x^1 e^{x^2} dy = \left[ye^{x^2}\right]_x^1
outer integral
\int_0^1 e^{x^2} - xe^{x^2} dx
Which is still problematic, and happens with all changes to the order of integration
But e^{x^2} = e^{y^2} so we can just replace e^{y^2} with e^{x^2} in the original problematic integral.
So
2 \times \int_0^1 \int_0^x e^{x^2} dy dx = 2 \times \frac{1}{2}\left(e-1\right) = e - 1
Or
2 \times \int_0^1 \int_0^y e^{y^2} dx dy = 2 \times \frac{1}{2}\left(e-1\right) = e - 1
Anyhow, I wanted to get an approx. verification of this is Matlab.
The code I used to generate that graph is
[x,y] = meshgrid(0:0.01:1,0:0.01:1); % 0.01 increments
z = max(x^2,y^2);
surf(x,y,z)
so, I figure for a good approximation of the volume under that surface should be
sum(sum(z.*0.0001)); % element-wise multiplication of z by 0.01 x 0.01
But this gives 0.513433500000000 which is not e - 1.
Is my analytic solution incorrect or my numeric approximation method? Or both?
1. Homework Statement
Evaluate the integral
\int_0^1 \int_0^1 e^{max(x^2,y^2)}dydx
where max(x^2,y^2) is the larger of the numbers x2 and y2.
Assumption: I'm assuming that x2 and y2 are real valued.
Homework Equations
The Attempt at a Solution
I consider the region of integration thusly
There is symmetry about the line y = x. Below this line, the max value is of y squared, since for y < x, y2 > x2. And so above the line y = x, the max value is x squared.
This is true because 0 <= x <= 1 and 0 <= y <= 1.
Using Matlab to sketch the 3-D graph gets
This looks right, and we can see the symmetry.
Now, if we setup the region is that we just integrate over the triangle created by y=x dividing the square [0,1]x[0,1], knowing that we must multiply the result by 2 at the end, we could evaluate the integral
\int_0^1 \int_0^x e^{y^2} dy dx
Now, this is problematic, since we can't eval. this analytically.
We can change the order of integration, but this results in further evariable squared integrated with respect to said variable situations. For instance, in one arrangement we get
\int_0^1\int_x^1 e^{x^2} dy dx
inner integral
\int_x^1 e^{x^2} dy = \left[ye^{x^2}\right]_x^1
outer integral
\int_0^1 e^{x^2} - xe^{x^2} dx
Which is still problematic, and happens with all changes to the order of integration
But e^{x^2} = e^{y^2} so we can just replace e^{y^2} with e^{x^2} in the original problematic integral.
So
2 \times \int_0^1 \int_0^x e^{x^2} dy dx = 2 \times \frac{1}{2}\left(e-1\right) = e - 1
Or
2 \times \int_0^1 \int_0^y e^{y^2} dx dy = 2 \times \frac{1}{2}\left(e-1\right) = e - 1
Anyhow, I wanted to get an approx. verification of this is Matlab.
The code I used to generate that graph is
[x,y] = meshgrid(0:0.01:1,0:0.01:1); % 0.01 increments
z = max(x^2,y^2);
surf(x,y,z)
so, I figure for a good approximation of the volume under that surface should be
sum(sum(z.*0.0001)); % element-wise multiplication of z by 0.01 x 0.01
But this gives 0.513433500000000 which is not e - 1.
Is my analytic solution incorrect or my numeric approximation method? Or both?