Alora
- 2
- 0
Could somebody please help me with this problem? I am very confused with calculations for multiple pulleys, especially those with movable ones...
http://www.geocities.com/cdy12/pulleys.jpg
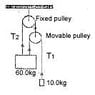
I am supposed to find the tension forces T1 and T2, as well as the acceleration of both masses.
I can do it if the whole thing is stationary, but as soon as the masses start accelerating I just don't know what to do. Please help!
http://www.geocities.com/cdy12/pulleys.jpg
I am supposed to find the tension forces T1 and T2, as well as the acceleration of both masses.
I can do it if the whole thing is stationary, but as soon as the masses start accelerating I just don't know what to do. Please help!