Navier Stokes EQ: Derivation in Integral Form

[Saladsamurai]

Hello! I am doing some review and it has occurred to me that I always confuse myself when I derive the the momentum equation in integral form. So I figure I will try to hammer through it here and ask questions as I go in order to clarify certain points. I know that there are many different approaches to this, but here is the one that I want to take:

- Finite control volume (CV) of fixed size and arbitrary shape, fixed in space

- Viscous flow

- I want to stay away from the Reynold's Transport Theorem
​

I will foreshadow where I think that I am having trouble: By definition, the momentum of a fluid element is given by m\mathbf{V}. That's all I will say for now since trying to explain my confusion is just more confusing than showing it

If we take an arbitrarily shaped CV fixed in space and look at a differential surface area ds we should be able to say something about the momentum flowing out of that area. Now the momentum of the fluid elements leaving across ds (which we will assume to be uniform) should be given by

\text{momentum} = \mathbf{p} = m\mathbf{V} \qquad(1)

Here is where it starts to get fuzzy for me: I usually see it written in terms of unit volume momentum: \rho\mathbf{V}. I am assuming that this is merely in anticipation of a volume integral at some point down the line and not some new definition for momentum of a fluid. Is this assumption correct? (Edit: I see now that the answer is no. It just works out that way.)

Moving forward. So we have this property p leaving at ds and we are interested in the rate at which it is leaving. Hmmm...I might be about ready to answer my own question. In order to find the rate at which it is leaving, the most sensible way to do so would be to find the rate at which mass is leaving the CV at ds and use that information along with the momentum per unit mass at ds. The outflow of mass at ds is given by \rho V_{ds} A_{ds} = \rho(\mathbf{V}\cdot\mathbf{n})dS=\rho\mathbf{V} \cdot \mathbf{dS} where n is the unit normal at ds and \mathbf{ds} = \mathbf{n}ds.

Now the momentum per unit mass is simply \frac{\mathbf{P}}{m}=\frac{m\mathbf{V}}{m}=\mathbf{V} so that the rate of momentum leaving at ds is given by:

\text{outflow} = (\dot{m})(\frac{\mathbf{p}}{m})=(\rho\mathbf{V} \cdot \mathbf{dS})(\mathbf{V})\qquad(2)

which I believe is what I am after here.

I will add onto this later for the sake of completion and because I am sure more questions will arise as I go along.

One question that I know is lurking is this: I vaguely remember a professor in some class in undergrad that we can think of momentum of a fluid being \dot{m}\mathbf{V} instead of m\mathbf{V} for a solid. I am not sure if we were meant to take this literally or just as a mental tool to help. I will have to dig a little deeper to answer that one, but for now I need to take the dog for a walk.

Crappy picture for a visual:

 

[boneh3ad]

If we take an arbitrarily shaped CV fixed in space and look at a differential surface area ds we should be able to say something about the momentum flowing out of that area. Now the momentum of the fluid elements leaving across ds (which we will assume to be uniform) should be given by

\text{momentum} = \mathbf{p} = m\mathbf{V} \qquad(1)

I strongly advise not using p for momentum in the context of fluids given the ambiguity it creates with pressure.

Here is where it starts to get fuzzy for me: I usually see it written in terms of unit volume momentum: \rho\mathbf{V}. I am assuming that this is merely in anticipation of a volume integral at some point down the line and not some new definition for momentum of a fluid. Is this assumption correct? (Edit: I see now that the answer is no. It just works out that way.)

Probably the best explanation of why we work with momentum per unit volume is due to the fact that this quantity is intensive and so is scale-invariant. Momentum is an extensive quantity, so you would have a hard time developing any assumptions about a generalized system if the quantity you are using depends on the size of the element or the control volume.

Moving forward. So we have this property p leaving at ds and we are interested in the rate at which it is leaving. Hmmm...I might be about ready to answer my own question. In order to find the rate at which it is leaving, the most sensible way to do so would be to find the rate at which mass is leaving the CV at ds and use that information along with the momentum per unit mass at ds. The outflow of mass at ds is given by \rho V_{ds} A_{ds} = \rho(\mathbf{V}\cdot\mathbf{n})dS=\rho\mathbf{V} \cdot \mathbf{dS} where n is the unit normal at ds and \mathbf{ds} = \mathbf{n}ds.

Now the momentum per unit mass is simply \frac{\mathbf{P}}{m}=\frac{m\mathbf{V}}{m}=\mathbf{V} so that the rate of momentum leaving at ds is given by:

\text{outflow} = (\dot{m})(\frac{\mathbf{p}}{m})=(\rho\mathbf{V} \cdot \mathbf{dS})(\mathbf{V})\qquad(2)

which I believe is what I am after here.

This is kind of an odd way to go about it but it does physically make sense.

One question that I know is lurking is this: I vaguely remember a professor in some class in undergrad that we can think of momentum of a fluid being \dot{m}\mathbf{V} instead of m\mathbf{V} for a solid. I am not sure if we were meant to take this literally or just as a mental tool to help.

At the moment I don't see how that makes any sense. That would actually be the rate of change of momentum in the system under steady flow conditions.

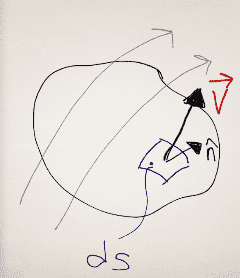
- Finite control volume (CV) of fixed size and arbitrary shape, fixed in space

- Viscous flow

- I want to stay away from the Reynold's Transport Theorem
​

This is unfortunate because the Reynolds Transport Theorem is a powerful tool and makes what you did much easier.

 

[Saladsamurai]

Hi boneh3ead Thanks for reading.

I strongly advise not using p for momentum in the context of fluids given the ambiguity it creates with pressure.



Probably the best explanation of why we work with momentum per unit volume is due to the fact that this quantity is intensive and so is scale-invariant. Momentum is an extensive quantity, so you would have a hard time developing any assumptions about a generalized system if the quantity you are using depends on the size of the element or the control volume.

Great explanation! Makes sense.

This is kind of an odd way to go about it but it does physically make sense.

Funny to me that you find it odd and making physical sense. I always like to take the physical approach to things and see what happens. All I did was apply the definition of momentum to a fluid element. What is odd?

At the moment I don't see how that makes any sense. That would actually be the rate of change of momentum in the system under steady flow conditions.

Agreed. Perhaps it was a special case that reduced to that expression.

This is unfortunate because the Reynolds Transport Theorem is a powerful tool and makes what you did much easier.

Yes I know! I don't like making it easy. RTT kind of sucks the physical intuition out it for me. I don't want to 'convert' equations for systems into equations for CV's just yet. I like to take the long road first.

Thanks again for your input.

 

[boneh3ad]

Funny to me that you find it odd and making physical sense. I always like to take the physical approach to things and see what happens. All I did was apply the definition of momentum to a fluid element. What is odd?

It is just not a, shall we say, conventional way of going about it. That doesn't make it wrong or any other method less physically correct, just different.

Yes I know! I don't like making it easy. RTT kind of sucks the physical intuition out it for me. I don't want to 'convert' equations for systems into equations for CV's just yet. I like to take the long road first.

Just prove the RTT then and then you have everything all ready-made for you. If you physically understand the RTT then you, by transitivity, physically understand why it works for quantities it is applied to like mass, momentum or energy.

Of course I respect the approach you prefer, and if that is the way you learn best, then carry on. You can't argue with that.

 

[Saladsamurai]

It is just not a, shall we say, conventional way of going about it. That doesn't make it wrong or any other method less physically correct, just different.

Yeah. I was just thinking of all of the different ways I have seen this derived and guess you are right; I have not seen my way before. I think all I did was reverse the horse and cart. Instead of starting on the basis on an intensive property, I started with an extensive and then half way through transitioned to intensive. Now I see that by anticipating this transition we can just start off with an intensive property and it is more general in its scalability.

Just prove the RTT then and then you have everything all ready-made for you. If you physically understand the RTT then you, by transitivity, physically understand why it works for quantities it is applied to like mass, momentum or energy.

Of course I respect the approach you prefer, and if that is the way you learn best, then carry on. You can't argue with that.

I know what you mean. I have done this before, but somehow always muckle myself up. Thanks again for the input!