jac7
- 20
- 0
I need to find the Fourier transform to this function
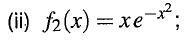 and I'm really stuck, because i tried substituting it into the Fourier transform equations but i started to get a really long integral that got out of hand!
and I'm really stuck, because i tried substituting it into the Fourier transform equations but i started to get a really long integral that got out of hand!
i also know that
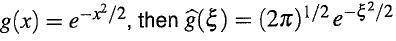 but i don't know how to incorporate it into finding the Fourier transform!
but i don't know how to incorporate it into finding the Fourier transform!
If someone could help me get started or give me some tips on easy steps for find the Fourier transform in general it would be much appreciated as my lecturer is away for easter!
Thanks!
i also know that
If someone could help me get started or give me some tips on easy steps for find the Fourier transform in general it would be much appreciated as my lecturer is away for easter!
Thanks!