Ah, a picture is gradually forming... I try (not always successfully) to keep an open mind, so it takes a while to focus on the situation at hand

. The link helps (especially the pictures).
Even the simplest case is already riddled with opportunites for hideous complications. Simplest case meaning: L is the length of both wires (H1 = H2 -- hey wasn't that already somewhere ?) and in addition: L ##\gg## r and ##\theta \ll 1##. In other words (as you said), the oscillations occur in a horizontal plane.
All the ##\approx## have to be satisfied !
Conveniently the link gives an expression for ##T## in this simplest case. Were you able to verify their equation (8) ? and to answer questions Q2, 3, 4 ?
---
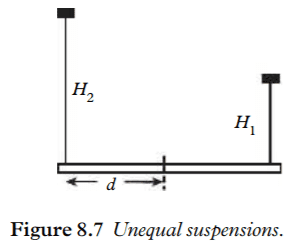
And then (now) your teacher (or you all alone by yourself ?) is making life difficult by making ##H_1 \ne H_2##. I can imagine a small clamp on the stand on the right in figure 3 that produces that effect:
So that now point P is fixed and H2 (in post #3

) is less than H1
As you see I only shortened H2 by a very small amount so that all the ##\approx## can still be satisfied. (In an initial stage I worried about a case like the entire length of H2 ony a few cm and had to shiver...).
Are we still in agreement about the setup ?My interpretation: 5 different positions of point P. Right ?
And a speculative deduction: you have to try it, so you haven't done it yet ?You could go through the steps of the derivation once more, but my level of abstraction is exceeded already, ...
Maybe split up equation (6) $${d^2\theta\over dt^2} + \left ( mgr^2 \over IL\right ) = 0 \qquad\rightarrow\qquad
{d^2\theta\over dt^2} + \left ( mgr^2 \over 2I\right ) \left ({1\over L_1} + {1\over L_2} \right ) = 0$$ but I don't have a good feeling about it...
so I would have to fall back to experimentation instead of theorizing.
 ) ?
) ? ##\qquad## !
##\qquad## !