Net electric flux through torus

AI Thread Summary
To find the net electric flux through a torus, apply Gauss's law, which states that the net flux is equal to the enclosed charge divided by the permittivity of free space. The problem indicates an enclosed charge of -1 nC, making the calculation straightforward once the area is determined. However, the lack of radius information complicates finding the area for the torus. The discussion emphasizes that the torus is a closed surface with both inner and outer surfaces. Overall, understanding Gauss's law is crucial for solving this problem effectively.
dtesselstrom
Messages
29
Reaction score
0

Homework Statement


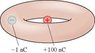
What is the net electric flux through the torus (i.e., doughnut shape) of the figure



Homework Equations



net flux= E*A I believe is needed

The Attempt at a Solution


I don't know how to do this problem at all. I feel like I don't have enough information to calculate the answer. Any advice as how to start this problem because I don't have the radius of the objects so how can I figure out the area.
 

Attachments

  • knight_Figure_27_22.jpg
    knight_Figure_27_22.jpg
    5 KB · Views: 1,945
Physics news on Phys.org
Use Gauss's law. The enclosed charge is - 1 nC if you choose the torus as the closed surface. It is a closed surface since it has an outer and inner surface and one cannot pass from the one to the other.
 
andrevdh said:
Use Gauss's law. The enclosed charge is - 1 nC if you choose the torus as the closed surface. It is a closed surface since it has an outer and inner surface and one cannot pass from the one to the other.

I had the same problem! you are right! thanks~
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Electric Field Flux Question
Replies
4
Views
701
Is Electric Flux Through a Half Sphere Zero According to Gauss' Law?
Replies
20
Views
3K
Flux through a cylindrical surface enclosing part of a sphere
Replies
9
Views
499
Flux of Electric field through sphere
Replies
2
Views
2K
Electric flux through ends of an imaginary cylinder
Replies
7
Views
2K
Calculating flux through a plane cutting two concentric cylinders
Replies
26
Views
1K
What is the Electric Flux through a Net in a Uniform Electric Field?
Replies
7
Views
5K
Gauss' law and flux concept issues
Replies
2
Views
1K
How Do You Calculate Net Electric Flux Through a Cube?
Replies
1
Views
6K
Electric Flux for a cube problem
Replies
8
Views
3K

Hot Threads

Recent Insights

Back
Top