Neutron Diffraction: Finding Wavelength of Neutron

[v_pino]

Homework Statement

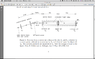
In an experimental setup (shown in attachment) like this for neutron diffraction, how do I find the wavelength of the neutron. It should be around 2nm.

Homework Equations

$$\lambda = \frac{h}{mv}=\frac{396}{v}$$

The Attempt at a Solution

I am having trouble with finding v of the neutron. Does it have to do with the total length of the tube?

 

[technician]

The only speed information in your diagrams states that the neutrons are 'thermal' neutrons. This means that they are in thermal equilibrium with the moderator.
In an online reference site I read that neutrons have a range of speeds but the accepted speed for thermal neutrons is 2200 m/s.
In the absence of any other information I would use this and at least get some sort of answer.