- #1
jpruim
- 6
- 0
I've been assigned the following problem for homework in my Electrical Engineering class:
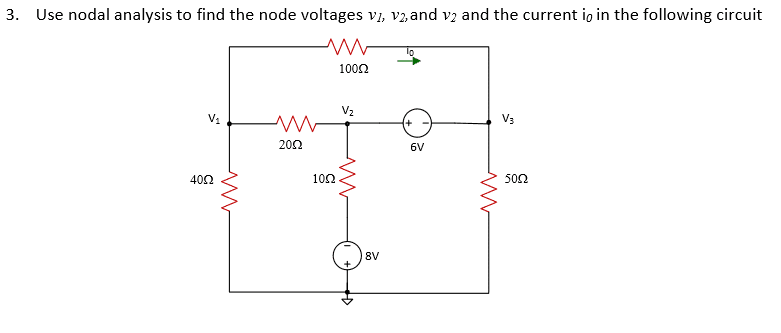
*Note, the duplicate v2 is supposed to be v3.
But I keep getting
v1 = 4.10V
v2 = 4.81V
v3 = -1.19V
and
i0 = 52.9mA
Every simulator I've put this into says it's wrong, yet I've attempted solving it about 12 times (consuming almost all my remaining notebook pages) and still get the same answers.
I can't post a copy of my written work since I currently don't have access to a scanner. However, I drew in arbitrary current directions and made sure to respect them for all calculations using KCL.
I have no idea what I'm doing wrong at this point. My professor just seems to get agitated when I ask what the convention is and his general response is "just do the current thing" or something vague like that. I don't think anyone in my class actually understands how to do this (except the class-repeaters).
I've been told by my friend to "always assume currents flow into a node. Ignore what's drawn. they always flow into nodes", but I've tried that at least 4 times. I've never gotten the answers my simulator provides me, regardless of how I solve it.
Is there any "convention" to solving these? Can anyone tell me what error I'm making so I don't make the same error on my exam?
*Note, the duplicate v2 is supposed to be v3.
But I keep getting
v1 = 4.10V
v2 = 4.81V
v3 = -1.19V
and
i0 = 52.9mA
Every simulator I've put this into says it's wrong, yet I've attempted solving it about 12 times (consuming almost all my remaining notebook pages) and still get the same answers.
I can't post a copy of my written work since I currently don't have access to a scanner. However, I drew in arbitrary current directions and made sure to respect them for all calculations using KCL.
I have no idea what I'm doing wrong at this point. My professor just seems to get agitated when I ask what the convention is and his general response is "just do the current thing" or something vague like that. I don't think anyone in my class actually understands how to do this (except the class-repeaters).
I've been told by my friend to "always assume currents flow into a node. Ignore what's drawn. they always flow into nodes", but I've tried that at least 4 times. I've never gotten the answers my simulator provides me, regardless of how I solve it.
Is there any "convention" to solving these? Can anyone tell me what error I'm making so I don't make the same error on my exam?