speakas
- 10
- 0
Homework Statement
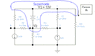
I have a circuit and I need to find the Nodal Equations that would mathematically describe the circuit, then proceed to finding the voltages at each node using Cramers rule and the currents at nodes 2 and 4. I don't think I would have much of a problem utilising Cramers rule. The problem I have right now is deriving the Nodal Equations.
However I would love to have the rest of my methods validated since I am simply unsure if I am on the right track or not
Homework Equations
The Attempt at a Solution
I am quite sure I have many errors in my attempted solution at deriving equations to describe the circuit. I am unsure what to do with the voltages sources.
Thank you very much in advance!